Python实现平稳时间序列ARMA模型详解

"本文主要探讨了如何利用Python进行平稳时间序列的建模，适用于数据分析和预测。文中通过详细的步骤和代码实例，展示了如何处理和分析时间序列数据，以构建ARMA模型进行预测。" 在时间序列分析中，平稳性是一个重要的概念。一个平稳时间序列的统计特性（如均值、方差和自相关性）不会随时间改变。对于非平稳序列，通常需要先进行差分或其他预处理，使其转化为平稳序列，以便进行有效的建模。Python提供了强大的库，如`pandas`用于数据处理，`statsmodels`用于统计建模，这些工具可以帮助我们实现这一目标。 一、平稳序列建模步骤 1. **样本自相关和偏自相关系数**：首先，我们需要计算序列的样本自相关系数（ACF）和样本偏自相关系数（PACF）。ACF描述了序列自身值之间的关联，而PACF则反映了当前值与滞后值之间的线性关系。`statsmodels`库的`acf`和`pacf`函数可以帮助计算这两个系数。 2. **选择ARMA模型**：根据ACF和PACF的截尾特性，我们可以选择合适的ARMA(p, q)模型。p是自回归项的阶数，q是移动平均项的阶数。截尾意味着在某个滞后点之后，相关系数接近于零。 3. **参数估计**：一旦模型确定，使用极大似然估计或最小二乘法来估计模型中的参数。 4. **模型有效性检验**：通过残差的ACF图和Ljung-Box检验等方法，检查模型是否有效。如果模型未通过检验，则需调整模型参数或选择不同的模型。 5. **模型优化**：尝试多种模型，对比AIC（Akaike Information Criterion）或BIC（Bayesian Information Criterion）等信息准则，选择最优模型。 6. **预测**：最后，使用选定的模型对序列的未来值进行预测。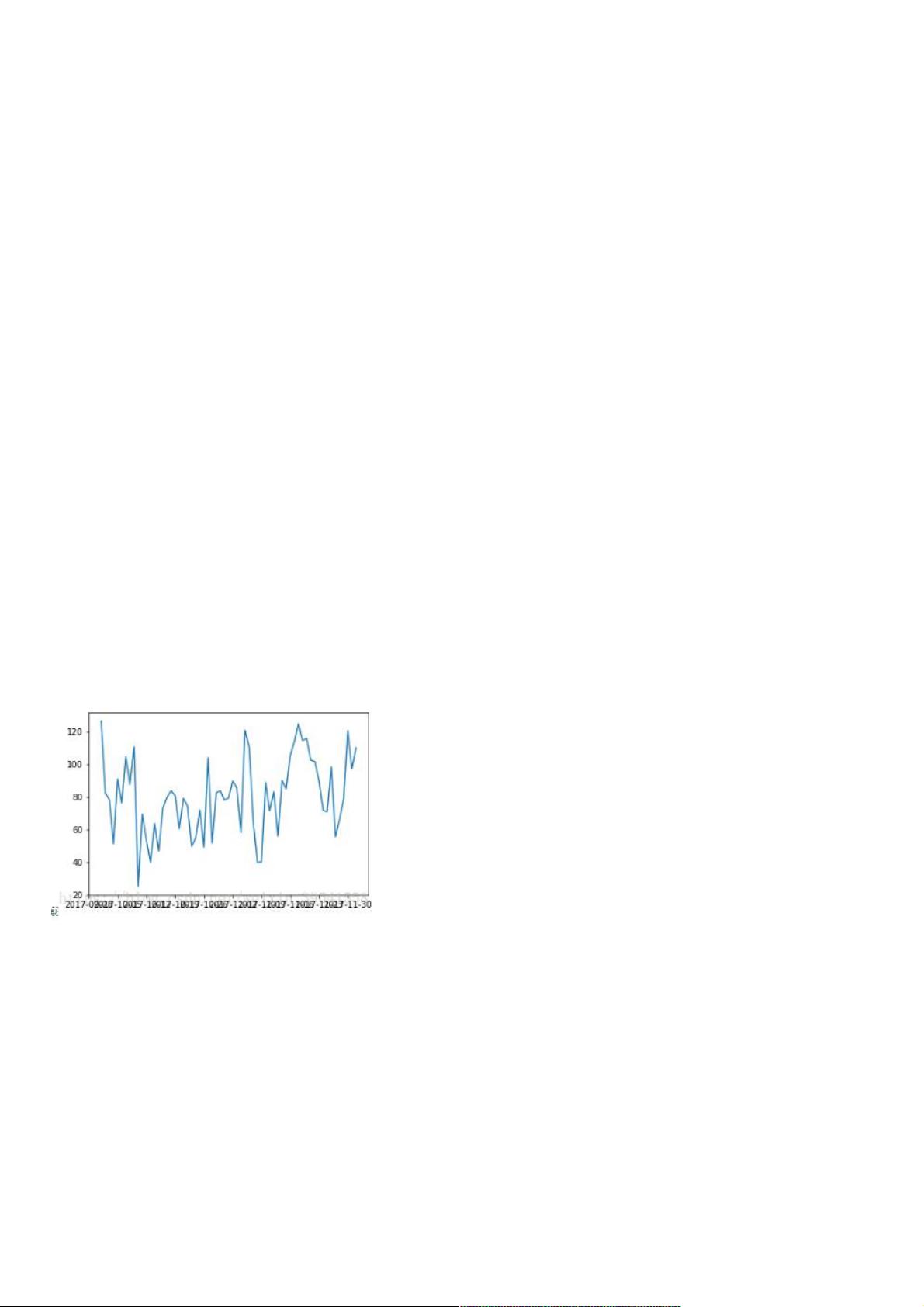 二、代码实现 在Python中，可以使用以下步骤实现： 1. **数据可视化**：`pandas`库的`head()`方法查看数据前几项，`matplotlib.pyplot.plot()`绘制序列图，帮助理解数据分布。 2. **平稳性检验**：通常使用ADF（Augmented Dickey-Fuller）检验判断序列是否平稳。如果ADF检验的p值小于显著性水平（如5%），则拒绝原假设，认为序列是平稳的。`statsmodels`库的`tsa.stattools.adfuller()`函数可执行此检验。 3. **差分**：若序列非平稳，可使用差分将其转换为平稳序列。例如，`timeseries.diff().dropna()`进行一次差分。 4. **模型拟合**：使用`statsmodels`的`ARMA`类拟合模型，例如`sm.tsa.ARMA(trainSeting, (p, q)).fit()`。 5. **模型评估与预测**：`residuals`属性可以获取模型残差，进一步进行ACF检验。`forecast()`方法可以生成预测值。 通过上述过程，我们可以有效地使用Python进行平稳时间序列的建模和预测，这对于经济、金融、气象等多个领域的数据分析都具有重要的实际应用价值。在实际操作中，应结合业务背景和数据特点，灵活运用这些方法和工具。