4
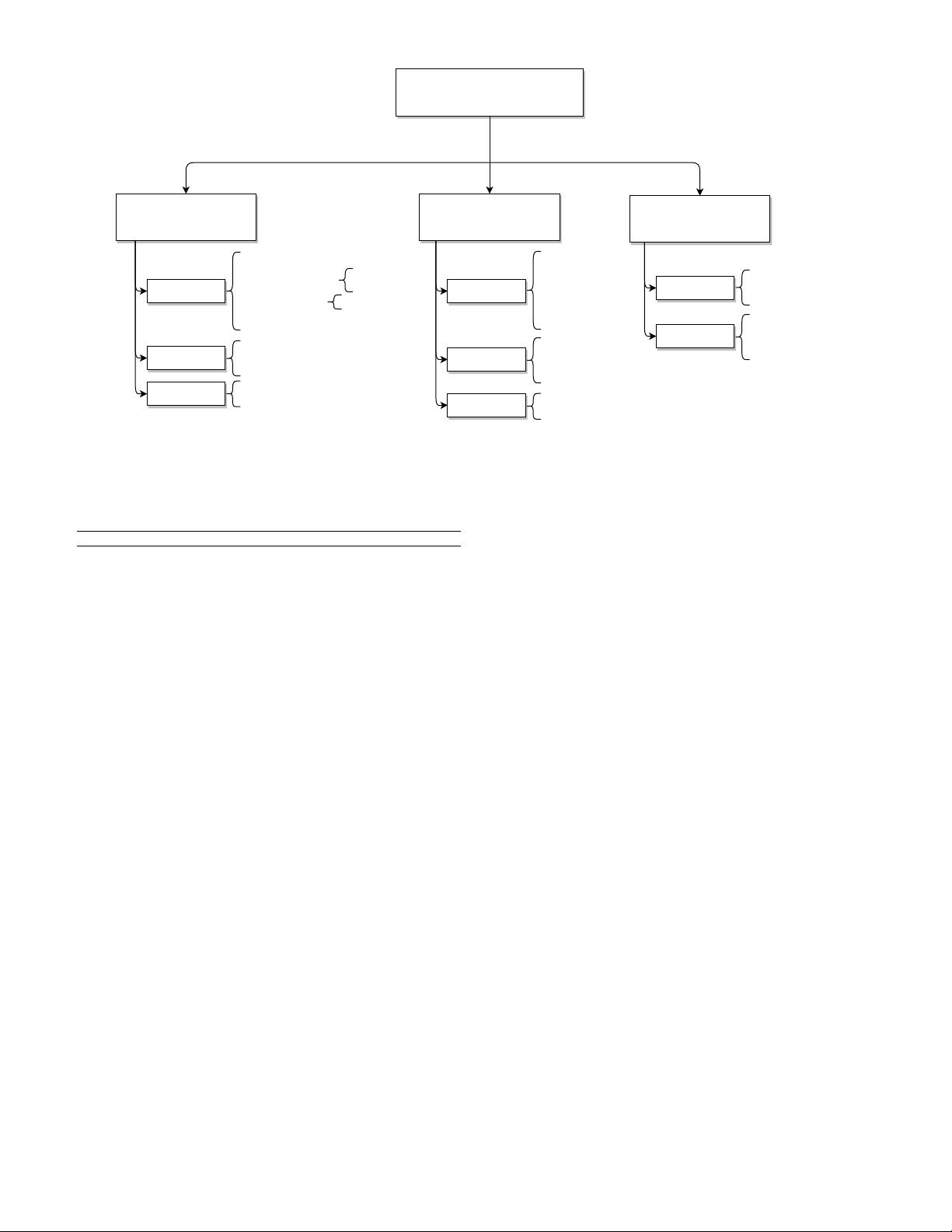
Attention Mechanisms
Feature-Related
Query-Related
General
Multiplicity
Levels
Representations
Scoring
Alignment
Multiplicity
Type
Dimensionality
Singular Features Attention
Coarse-Grained Co-Attention
Fine-Grained Co-Attention
Multi-Grained Co-Attention
Rotatory Attention
Single-Level Attention
Attention-via-Attention
Hierarchical Attention
Single-Representational Attention
Multi-Representational Attention
Additive Scoring
Multiplicative Scoring
Scaled Multiplicative Scoring
General Scoring
Biased General Scoring
Activated General Scoring
Similarity Scoring
Global/Soft Alignment
Hard Alignment
Local Alignment
Reinforced Alignment
Single-Dimensional Attention
Multi-Dimensional Attention
Basic Queries
Specialized Queries
Self-Attentive Queries
Alternating Co-Attention
Interactive Co-Attention
Parallel Co-Attention
Singular Query Attention
Multi-Head Attention
Multi-Hop Attention
Capsule-Based Attention
Fig. 3. A taxonomy of attention mechanisms.
TABLE 1
Notation.
Symbol Description
F Matrix of size d
f
× n
f
containing the feature vectors
f
1
, . . . , f
n
f
∈ R
d
f
as columns. These feature vectors
are extracted by the feature model.
K Matrix of size d
k
× n
f
containing the key vectors
k
1
, . . . , k
n
f
∈ R
d
k
as columns. These vectors are used
to calculate the attention scores.
V Matrix of size d
v
× n
f
containing the value vectors
v
1
, . . . , v
n
f
∈ R
d
v
as columns. These vectors are used
to calculate the context vector.
W
K
Weights matrix of size d
k
× d
f
used to create the K
matrix from the F matrix.
W
V
Weights matrix of size d
v
× d
f
used to create the V
matrix from the F matrix.
q Query vector of size d
q
. This vector essentially repre-
sents a question, and is used to calculate the attention
scores.
c Context vector of size d
v
. This vector is the output of the
attention model.
e Score vector of size d
n
f
containing the attention scores
e
1
, . . . , e
n
f
∈ R
1
. These are used to calculate the atten-
tion weights.
a Attention weights vector of size d
n
f
containing the at-
tention weights a
1
, . . . , a
n
f
∈ R
1
. These are the weights
used in the calculation of the context vector.
orthogonal dimensions of an attention model. An attention
model can consist of a combination of techniques taken
from any or all categories. Some characteristics, such as
the scoring and alignment functions, are generally required
for any attention model. Other mechanisms, such as multi-
head attention or co-attention are not necessary in every
situation. Lastly, in Table 1, an overview of used notation
with corresponding descriptions is provided.
3.1 Feature-Related Attention Mechanisms
Based on a particular set of input data, a feature model
extracts feature vectors so that the attention model can
attend to these various vectors. These features may have
specific structures that require special attention mechanisms
to handle them. These mechanisms can be categorized to
deal with one of the following feature characteristics: the
multiplicity of features, the levels of features, or the repre-
sentations of features.
3.1.1 Multiplicity of Features
For most tasks, a model only processes a single input, such
as an image, a sentence, or an acoustic sequence. We refer
to such a mechanism as singular features attention. Other
models are designed to use attention based on multiple
inputs to allow one to introduce more information into the
model that can be exploited in various ways. However, this
does imply the presence of multiple feature matrices that
require special attention mechanisms to be fully used. For
example, [32] introduces a concept named co-attention to
allow the proposed visual question answering (VQA) model
to jointly attend to both an image and a question.
Co-attention mechanisms can generally be split up
into two groups [33]: coarse-grained co-attention and
fine-grained co-attention. The difference between the two
groups is the way attention scores are calculated based on
the two feature matrices. Coarse-grained attention mecha-
nisms use a compact representation of one feature matrix
as a query when attending to the other feature vectors.
Fine-grained co-attention, on the other hand, uses all feature
vectors of one input as queries. As such, no information is
lost, which is why these mechanisms are called fine-grained.
As an example of coarse-grained co-attention, [32] pro-
poses an alternating co-attention mechanism that uses the
context vector (which is a compact representation) from one
attention module as the query for the other module, and
vice versa. Alternating co-attention is presented in Fig. 4.
Given a set of two input matrices X
(1)
and X
(2)
, features
are extracted by a feature model to produce the feature
matrices F
(1)
∈ R
d
(1)
f
×n
(1)
f
and F
(2)
∈ R
d
(2)
f
×n
(2)
f
, where d
(1)
f









