GMSK简化接收机设计与MATLAB仿真

"本文主要介绍了GMSK调制信号的简化接收机的理论与过程，包括Viterbi算法和Laurent分解的原理。接着通过Matlab进行仿真，并展示仿真结果，最后对Simplified Receiver解调GMSK信号的性能进行了分析。关键词：GMSK，简化接收机，Viterbi算法，Laurent分解。" GMSK（Gaussian Minimum Shift Keying）是一种连续相位调制（Continuous Phase Modulation，CPM）技术。根据调制脉冲的持续时间，CPM可以分为全响应和部分响应两类。在全响应CPM中，当调制指数为0.5且调制频率脉冲任意时，形成了一种广义MSK的形式。而具有矩形频率脉冲但任意调制指数的全响应方案被称为连续相位频率移键调制（Continuous Phase Frequency-Shift Keying，CPFSK），实际上它是GMSK的前身。 GMSK调制的基本思想是将二进制数据流转换为相位连续的信号。在调制过程中，数据比特流控制一个低通滤波器的输入，该滤波器的输出就是GMSK调制信号。由于GMSK采用了高斯滤波器，因此它的频谱效率比普通的FSK更高，而且具有较好的抗干扰能力。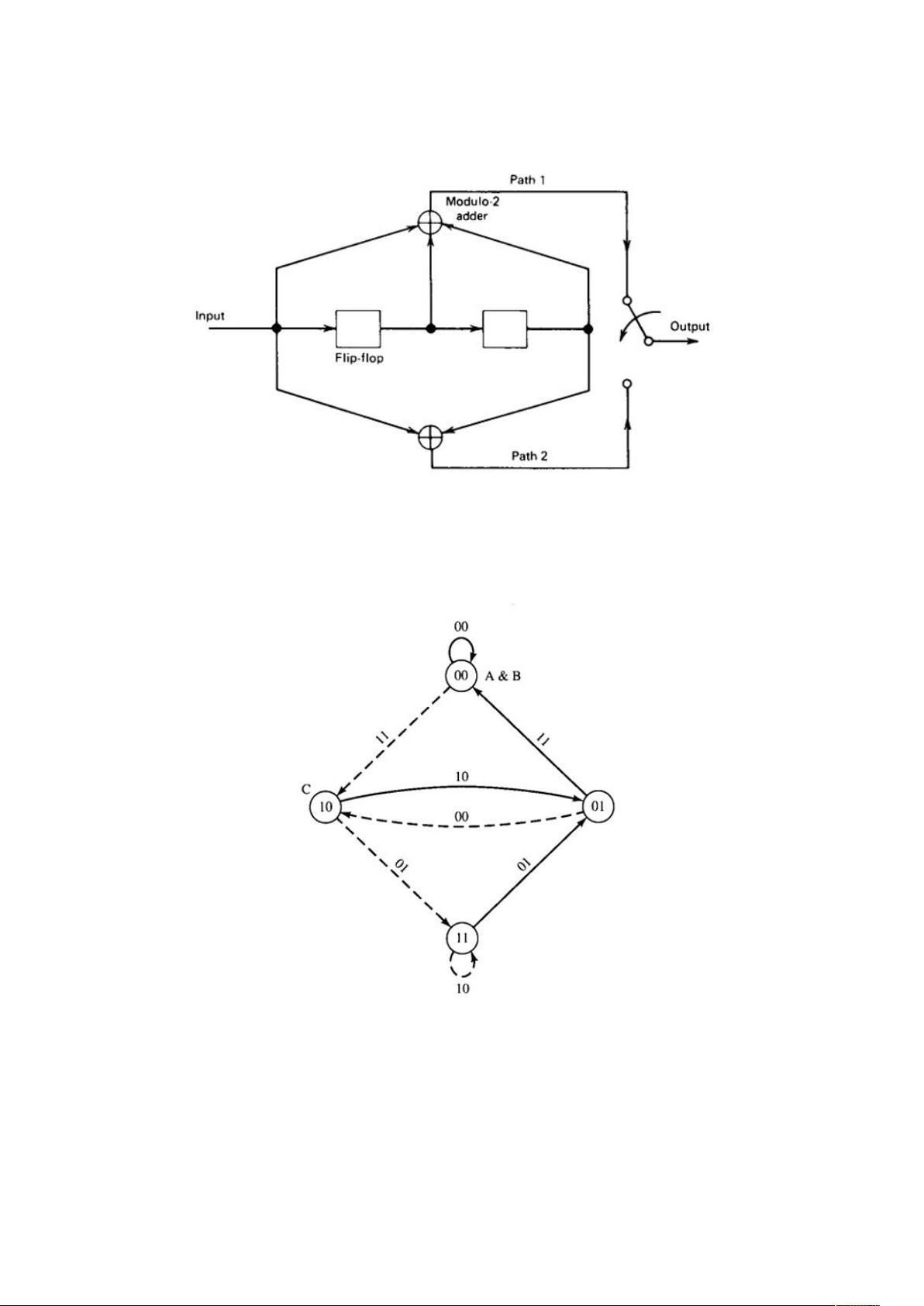 Viterbi算法在GMSK信号的解调中起着关键作用，它是一种在最大似然准则下进行硬判决的分组码最佳解码方法。Viterbi算法通过计算每个状态到当前时刻的最短距离，找出最有可能的码序列路径，从而实现对GMSK信号的有效解调。在噪声环境中，Viterbi算法能提供较高的误码率性能。 Laurent分解则是一种在数字信号处理中的数学工具，特别是在处理环状系统或循环移位相关性时非常有用。在GMSK信号的处理中，Laurent分解可能用于分析信号的循环特性，帮助优化解调过程。 Matlab作为一种强大的数值计算和仿真工具，被广泛用于GMSK信号的模拟和分析。通过编写Matlab代码，可以实现GMSK信号的生成、传输、噪声添加以及解调等过程的仿真，进而观察并分析其性能。仿真结果可以帮助理解理论分析，验证算法的正确性，同时对系统参数进行优化。 在本文中，作者不仅阐述了GMSK调制和解调的基本理论，还通过Matlab进行了实际的仿真，展示了仿真结果。通过对Simplified Receiver解调GMSK信号的性能分析，为实际应用提供了参考。这样的研究对于理解GMSK调制机制，以及在实际通信系统中优化接收机设计具有重要意义。