立体图像质量评估：联合双目能量对比感知方法

100 浏览量更新于2024-08-26 收藏 2.91MB PDF 举报

"联合双目能量对比感知用于立体图像质量评估" 这篇研究论文深入探讨了立体图像质量评估的新方法，特别是如何利用人的双目视觉系统（BVS）来更准确地评估立体图像的质量。立体图像，即3D图像，是通过为左右眼提供略有差异的图像来创造深度感知的。双目视觉系统在处理这些图像时，会经历两种主要的双目交互现象：双眼融合和双眼竞争。双眼融合是指大脑将来自左右眼的不同图像合并成一个单一、有深度感的图像。而双眼竞争则是在两个图像信息不完全匹配时，大脑可能会交替关注一个眼睛的图像，而不是整合两者。这两种机制在立体图像质量评估中起着关键作用，因为它们直接影响观看者的视觉体验和图像的可接受度。论文中提出了一种新的全参考立体图像质量评估模型，称为“联合双目能量对比感知”（Joint Binocular Energy-Contrast Perception）。这个模型考虑了双眼能量对比，即比较左右眼接收到的图像的亮度和对比度信息。这种比较有助于模拟人眼如何处理立体图像中的差异，以评估图像的整体质量。为了构建这个模型，作者可能采用了视觉敏感度函数（CSF，Contrast Sensitivity Function）的概念。CSF描述了人类视觉系统对不同空间频率和对比度的敏感度，这在理解和预测人眼对图像质量的感知上非常有用。通过结合CSF和双眼能量对比，该模型可以更精确地捕捉到立体图像中可能引起视觉不适或质量下降的因素。此外，论文可能还包含了实验设计和结果分析，通过与现有的立体图像质量评估方法进行对比，验证了新模型的有效性和优越性。这些实验可能包括主观评价，如双耳合成质量评估（DSQA，Double Stimulus Quality Assessment）或单耳质量评估（SSQA，Single Stimulus Quality Assessment），以及客观评价，如基于模型的评估方法。这篇研究论文为立体图像质量评估提供了一个创新的、基于生物视觉机制的方法，这有助于提高3D内容的制作和显示标准，确保观众获得更佳的视觉体验。对于3D图像处理、视频编码、显示技术以及人机交互等领域的发展具有重要的理论和实践意义。

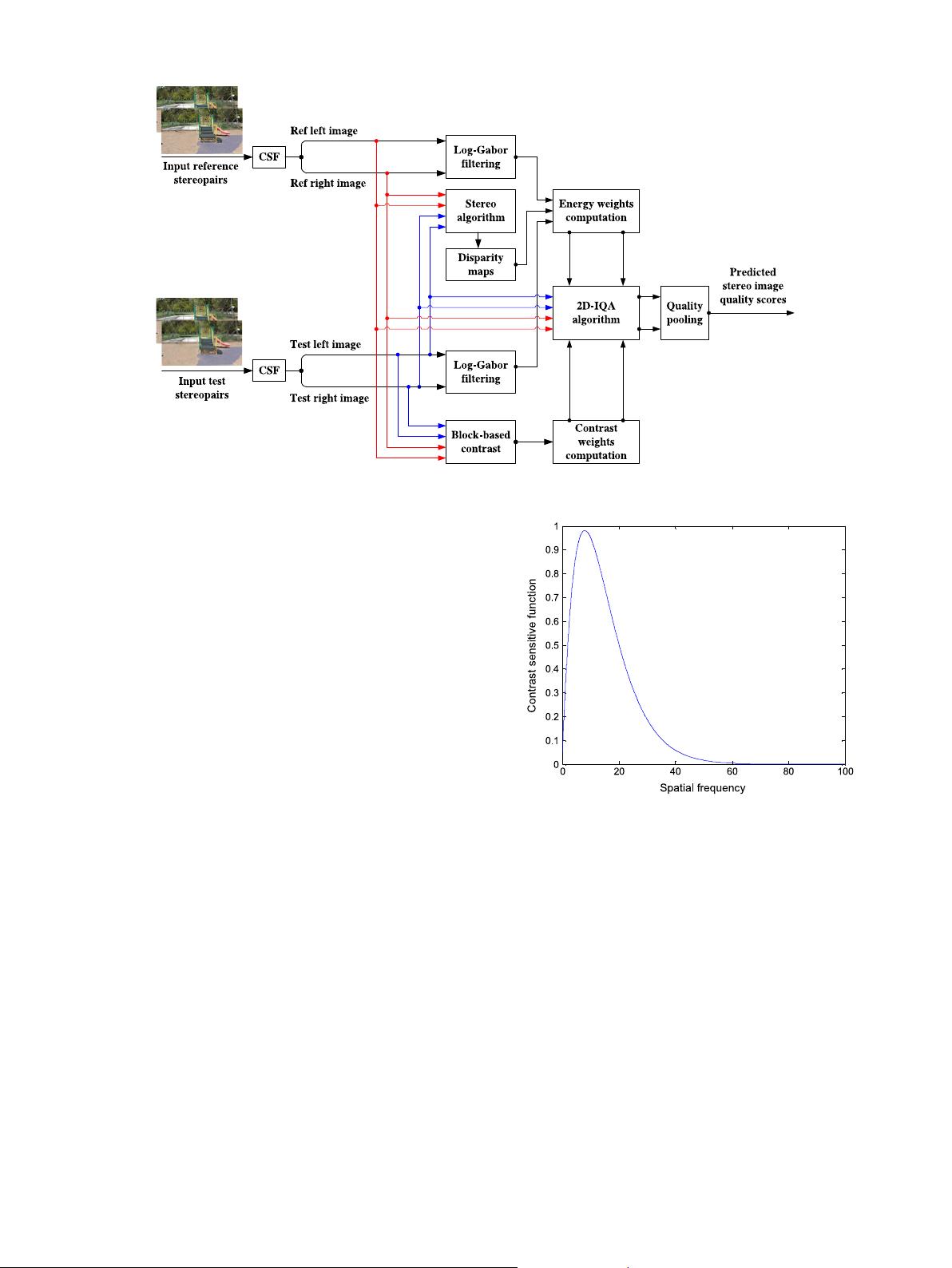
J. Ma et al. Signal Processing: Image Communication 65 (2018) 33–45

Fig. 1. Proposed FR quality assessment framework for stereoscopic images.

2.1. Contrast sensitivity function filtering

Since there are some inherent limitations with respect to the visibil-

ity of stimuli, the BVS is not equally sensitive to all stimuli. According

to [28], the binocular visual sensitivity to stimulus at different spatial

frequencies is different which could be modeled by an empirical CSF.

A widely-used CSF is the one introduced by Mannos and Sakrison [29]

with adjustments specified by Daly [30]. This CSF, 𝐻(𝑓, 𝜃), is defined

𝐻(𝑓, 𝜃) =



2.6(0.0192 + 𝜆𝑓

𝜃

) exp[−(𝜆𝑓

𝜃

)

1.1

], if𝑓 ≥ 𝑓

𝑝𝑒𝑎𝑘

𝑐∕ deg

0.981 otherwise

(1)

where 𝑓 denotes the radial spatial frequency in cycles per degree of

visual angle (c/deg),𝜃 ∈

[

−𝜋, 𝜋

]

denotes the orientation, and 𝑓

𝜃

𝑓∕[0.15 cos(4𝜃 + 0.85)] accounts for the oblique effect. Fig. 2 shows the

resulting curves called Mannos and Sakrison’s CSF. From Fig. 2, we can

see that the BVS is sensitive to a limited range of frequencies. Therefore,

in this paper, we consider variations in sensitivity to spatial frequency by

applying the CSF filtering independently to each image of the reference

and distorted stereopairs. Suppose we apply the CSF filtering to the

luminance image



𝐿

𝑙

. This CSF filtering is performed in the frequency

domain via



𝐼 = 𝐹

−1





H(𝑢, 𝑣) × 𝐹 [



𝑙

]



(2)

where 𝐹 [.] and 𝐹

−1

[.] denote the DFT and inverse DFT, respectively. The

quantity



H(𝑢, 𝑣) denotes a DFT based version of 𝐻(𝑓, 𝜃), where 𝑢, 𝑣 are

the DFT indices. Here, the CSF is further adjusted as described in [31]

to have a lowpass profile by explicitly setting frequencies below 𝑓

𝑝𝑒𝑎𝑘

to 0.981, which is the maximum value of 𝐻

(

𝑓, 𝜃

)

as determined by 𝜆.

According to [31–33], we have set 𝜆 = 0.114, resulting in a peak at

a frequency of 𝑓

𝑝𝑒𝑎𝑘

≈ 8𝑐∕ deg, which is measured before forcing the

lowpass profile within the range of 1 to 8 c/deg typically reported for

CSF.

2.2. The weights of binocular energy perception

From a biological point of view, the stereoscopy can be defined as

the association of two eyes in the visual analysis of the same region of

the scene. If the information received by the two eyes is compatible, the

brain combines their inputs in a way that yields a stable, unitary percept.

Fig. 2. Spatial frequency response curve of CSF.

This process of combination, known as ‘‘binocular fusion’’. However,

for merging of slightly different images from the two eyes, arising from

binocular disparity, into a single stereoscopic perception, the BVS needs

to decide which points in the left and right images correspond to the

same physical location. In [34], Banks et al. pointed out that the BVS

might solve the correspondence problem by using an approach similar to

cross-correlation. Also, several electro-physiological experiments have

provided detailed descriptions of the response properties of binocular

neurons in the primary visual cortex [35,36]. Interestingly, these re-

sponses of the receptive field are well described by binocular energy

model [37,38]. Since the binocular energy model provides a good

description of the first stages of cortical binocular processing, many

previous studies adopted binocular energy model for diverse 3D visual

signal processing [39,40]. For example, Bensalma et al. [39] proposed

a stereoscopic color image coding approach by using binocular energy

model. Furthermore, in stereo vision, binocular energy response not only

depends on the amplitude and phase but also relies on the disparity

information inputs. Because of the left and right images do not have the

same position, the left view response 𝑅

𝑙

(𝑥, 𝑦) is the equal of a shifted

剩余12页未读，继续阅读

weixin_38562026

粉丝: 3
资源: 949

立体图像质量评估：联合双目能量对比感知方法

基于深度学习的无参考立体图像质量评价.pdf

电信设备-基于梯度信息指导双目视图融合的立体图像质量评价方法.zip

双目感知下立体图像质量评估新方法：简化参考与BPI应用

立体图像质量评估：双目能量响应方法

通过学习基于非负矩阵分解的彩色视觉特征并考虑双目相互作用来评估立体图像质量

通过学习双目感受野特性对立体图像进行全参考质量评估

基于卷积神经网络的立体图像质量评价.pdf

模拟单双目感知的立体图像保真度指标

双目视觉特征驱动的立体图像全参考质量评估方法

立体图像质量评估：基于双目视觉特性的学习方法

最新资源