图的遍历：深度优先与广度优先搜索

"图的遍历1" 在计算机科学中，图是一种重要的数据结构，它可以用来表示对象之间的关系，如社交网络中的朋友关系、道路网络中的连接等。图由顶点（或节点）和边（连接顶点的线）组成，具有广泛的应用场景，包括网络路由、图像处理、推荐系统等。 图的遍历是访问图中所有顶点的过程，通常从一个指定的起点开始。这个过程旨在探索图的所有路径，同时避免陷入无限循环，特别是当图中存在回路时。为了处理回路问题，遍历算法会为每个顶点设置一个访问标志（mark），一旦顶点被访问过，它的标志就会被标记，确保同一顶点不会被重复访问。 遍历算法主要有两种：深度优先搜索（DFS，Depth-First Search）和广度优先搜索（BFS，Breadth-First Search）。 1. 深度优先搜索（DFS）： DFS 是一种递归策略，从起点开始，尽可能深地探索图的分支，直到到达一个无法进一步扩展的点（即，没有未访问的邻接顶点）。然后，它会回溯到上一个顶点，继续沿着另一个分支进行。DFS 使用栈来存储待访问的顶点，以处理回溯操作。这种方法的优点是在有向图中可以找到最短的路径，但不保证找到的是最短路径。 2. 广度优先搜索（BFS）： 与DFS不同，BFS 是一种层次遍历方法，从起点开始，首先访问与其相邻的所有未访问顶点，然后依次访问距离起点更远的顶点。BFS 使用队列来存储待访问的顶点，确保总是先访问距离起点近的顶点。这种方法在寻找两个顶点之间的最短路径时特别有用，特别是在无权图中。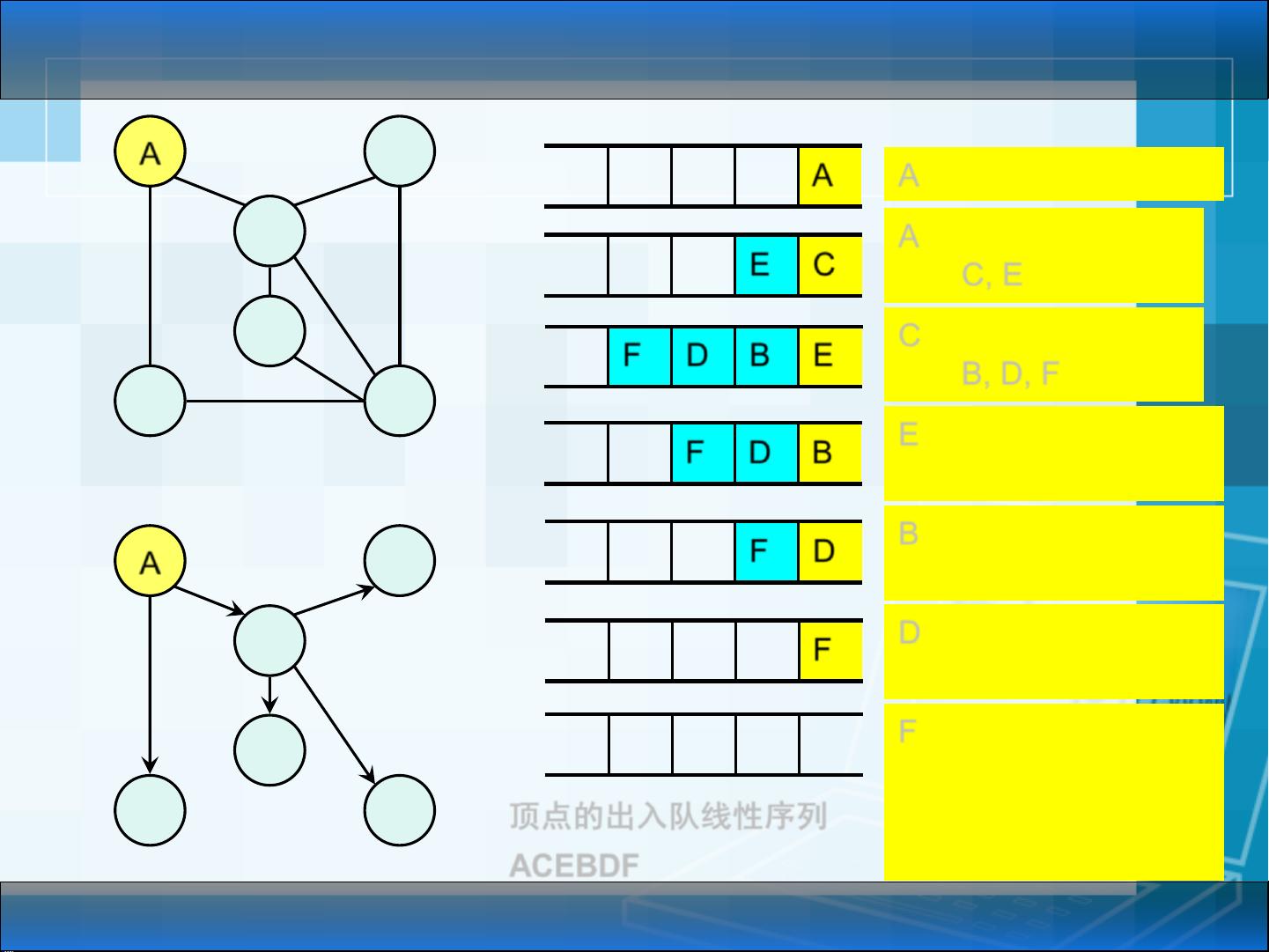 在BFS的过程中，我们通常会使用一个标志数组记录每个顶点是否已被访问，同时用一个队列来保存待处理的顶点。算法开始时，将起点放入队列，并将其标记为已访问。接着，每次从队列中取出一个顶点，访问它并将其所有未访问的邻接顶点加入队列。这个过程持续到队列为空，即所有可达的顶点都被访问过。 BFS 的伪代码如下： ```markdown BFS(G) 1. 初始化队列 Q 和访问标志数组 Mark，所有顶点标记为未访问 2. 将起点 v 入队 3. 当队列非空时，执行以下步骤： 1. 从队列中取出顶点 v 2. 访问顶点 v 3. 遍历 v 的所有邻接顶点 w，如果 w 未被访问，则将 w 入队 ``` 通过BFS，我们可以按照访问顺序输出图的所有顶点，从而获取到一种层次的顺序。 图的遍历是理解图论和算法设计的关键部分，无论是深度优先还是广度优先，它们都在解决实际问题中扮演着重要角色，比如寻找最短路径、检测环路、求解连通性等问题。熟练掌握这两种遍历方法对于提升算法设计能力和解决问题的能力至关重要。