suCAQR: A Simplified Communication-Avoiding
QR Factorization Solver Using the TBLAS
Framework
Weijian Zheng and Fengguang Song
Department of Computer Science
Indiana University Purdue University Indianapolis
Email: {wz26, fgsong}@iupui.edu
Lan Lin
Department of Computer Science
Ball State University
Email: llin4@bsu.edu
Zizhong Chen
Department of Computer Science
University of California at Riverside
Email: chen@cs.ucr.edu
Abstract—The scope of this paper is to design and implement
a scalable QR factorization solver that can deliver the fastest
performance for tall and skinny matrices and square matrices on
modern supercomputers. The new solver, named scalable univer-
sal communication-avoiding QR factorization (suCAQR), introduces
a simplified and tuning-less way to realize the communication-
avoiding QR factorization algorithm to support matrices of any
shapes. The software design includes a mixed usage of physical
and logical data layouts, a simplified method of dynamic-root
binary-tree reduction, and a dynamic dataflow implementation.
Compared with the existing communication avoiding QR fac-
torization implementations, suCAQR has the benefits of being
simpler, more general, and more efficient. By balancing the
degree of parallelism and the proportion of faster computational
kernels, it is able to achieve scalable performance on clusters of
multicore nodes. The software essentially combines the strengths
of both synchronization-reducing approach and communication-
avoiding approach to achieve high performance. Based on the
experimental results using 1,024 CPU cores, suCAQR is faster
than DPLASMA by up to 30%, and faster than ScaLAPACK by
up to 30 times.
Index Terms—high performance computing; computational
science application; performance analysis and optimization;
dataflow runtime system.
I. INTRODUCTION
QR factorization is a fundamental computational kernel for
many important scientific, engineering, and big data analytics
applications. It has been applied to solving linear systems,
least-squares problems, linear regression problems, and the
production function modeling, as well as assessing the con-
ditioning of these problems [1]–[3]. The QR factorization of
a matrix A of dimension m × n (m ≥ n) takes the form of
A = QR, where Q is an m × m orthogonal matrix, and R
(=Q
T
A) is an upper triangular matrix with zeros below its
diagonal. The design and implementation of more scalable
QR factorizations will accelerate a wide range of domain
applications.
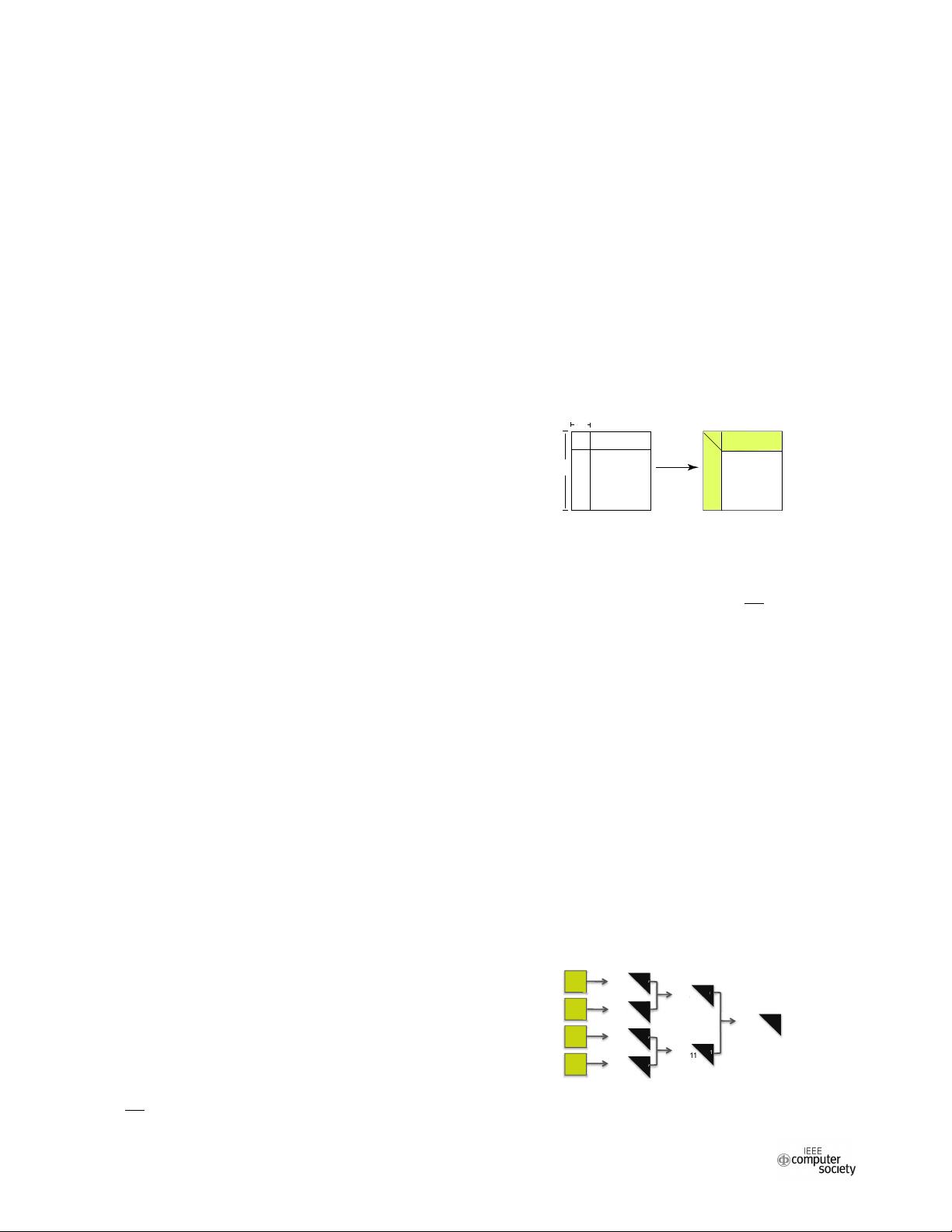
The most widely used parallel algorithm to solve QR
factorizations is the block QR factorization algorithm used
by the de facto standard ScaLAPACK library [4], [5]. As
displayed in Figure 1, matrix A is divided into a thin panel
(i.e.,
A
11
A
21
) of dimension M × NB, a block of rows A
12
, and
R11
V21
R12
A22
A11
A21
A12
A22
M
NB
Fig. 1. The classic block QR factorization algorithm used by ScaLAPACK.
a trailing submatrix A
22
. The block algorithm first applies
level 1 PBLAS subroutines to the panel (
A
11
A
21
), next it forms
the triangular factor from the panel, finally it uses level 3
PBLAS to factor A
12
and update A
22
. However, since the
panel is computed one column after another—resulting in a
large communication overhead and surface-to-volume ratio —
the block algorithm does not scale well for tall and skinny
matrices (i.e., matrices with much more rows than columns).
To reduce the large communication overhead with tall and
skinny matrices, Demmel et al. then designed an algorithm
called Communication-Avoiding QR factorization (CAQR) [6]–
[8]. As explained in Figure 2, instead of computing a sequence
of column-by-column operations, CAQR can perform a set of
level 3 BLAS operations in the panel. Then it merges the
output of the level 3 BLAS operations to get the final factor
R. Not only does the algorithm convert level 1 BLAS to
level 3 BLAS, but also it significantly reduces the number of
communication messages. The original work of Demmel et al.
[6] offered an estimated performance speedup of CAQR. Later,
Song et al. [9] developed the first parallel implementation of
CAQR, which is referred to as distributed tiled CAQR [9].
A
0
A
1
A
2
A
3
Q
00
R
00
Q
10
1
R
10
Q
20
R
20
Q
30
R
30
Q
01
R
01
Q
11
R
11
Q
02
R
02
Fig. 2. Communication-Avoiding QR (CAQR) performs level 3 BLAS on the
panel (i.e., A
0
, A
1
, A
2
, A
3
) followed by a parallel reduction.
2016 IEEE 22nd International Conference on Parallel and Distributed Systems
1521-9097/16 $31.00 © 2016 IEEE
DOI 10.1109/ICPADS.2016.142
1092









