遗传算法在随机优化中的应用

"基于遗传算法的随机优化搜索" 遗传算法是一种模拟自然选择和遗传机制的全局优化方法，广泛应用于解决复杂的优化问题。在本资源中，主要介绍了遗传算法的基本概念、操作以及特点。 4.1 基本概念 1. 个体与种群 在遗传算法中，"个体"是对问题解决方案的抽象表示，每个个体代表搜索空间中的一个可能解。"种群"是由多个个体组成，类似于生物种群，它构成了搜索空间的一个小样本集。种群的大小和多样性对于算法的性能至关重要，因为它影响了算法探索解决方案空间的能力。 2. 适应度与适应度函数 适应度是衡量个体对问题环境适应程度的标准，相当于其解决问题的能力。适应度函数则是将个体映射到一个数值，这个数值反映了个体的优劣。通常，适应度值越高，个体被视为更优秀的解。适应度函数的设计直接影响到算法的收敛速度和找到最优解的能力。 3. 染色体与基因 染色体是问题个体的编码表示，通常以字符串形式存在，而基因是构成染色体的基本单元。在实际应用中，基因可以代表问题的参数或者决策变量。 4. 遗传操作 遗传操作包括选择、交叉和变异，它们是遗传算法的核心步骤。 - 选择-复制：按照每个个体的适应度选择概率，从当前种群中挑选个体进行复制，形成下一代种群。这确保了适应度高的个体有更高的生存概率。 - 交叉：也称为交换或杂交，两个或多个个体的部分基因（染色体段）被互换，产生新的个体，增加种群的多样性。 - 变异：随机改变部分基因的值，防止算法过早收敛，维持种群的探索能力。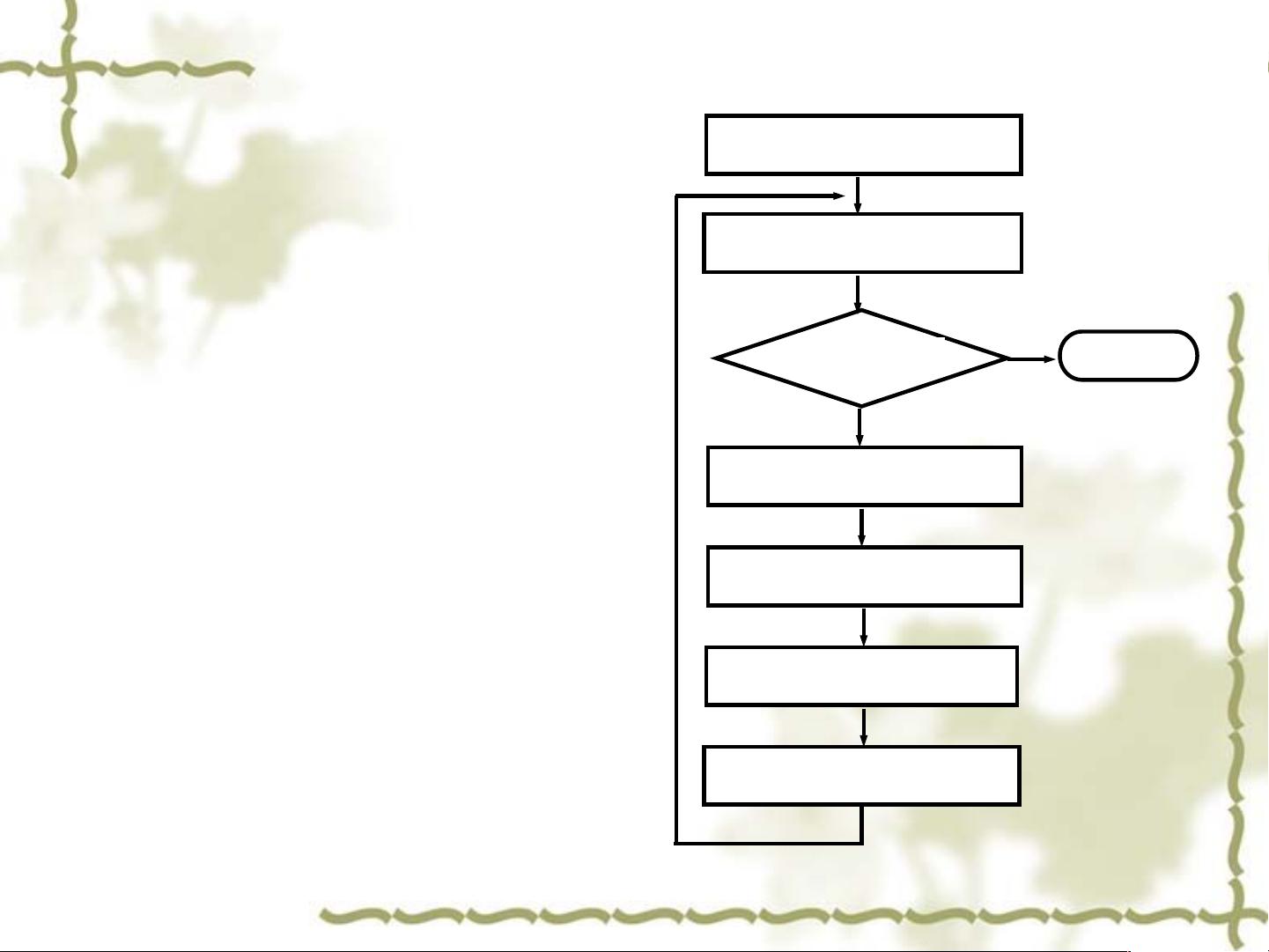 4.2 基本遗传算法 遗传算法的基本流程包括生成初始种群、计算适应度、选择-复制、交叉和变异等步骤，不断迭代直至满足停止条件（如达到预设的迭代次数、适应度阈值等）。这个过程模拟了生物进化的过程，通过自然选择和随机变异来寻找最优解。 4.3 遗传算法的应用举例 遗传算法可以用于各种领域，如机器学习中的参数调优、工程设计中的优化问题、组合优化问题（如旅行商问题）等。 4.4 遗传算法的特点与优势 遗传算法的主要优点包括： - 全局搜索能力：由于其随机性和多样性保持，能有效地跳出局部最优，寻找全局最优。 - 自适应性：算法无需对问题的先验知识，适用于多模态和非线性问题。 - 并行处理：可以并行处理多个个体，提高计算效率。 - 解的多样性：通过种群保持多种解，可以得到一组近似最优解，而非单个解。 然而，遗传算法也可能面临一些挑战，如可能会陷入早熟收敛、需要合适的参数设置等。因此，在实际应用中，通常需要对算法进行调整和优化，以适应特定的问题。