回溯法解决N皇后问题

"本文主要介绍了回溯法作为解决一系列选择组成的复杂问题的策略，并通过N个皇后问题举例说明了回溯法相比于暴力法的优势。回溯法是一种深度优先搜索策略，通过即时检查不可行性来避免无效的选择，从而提高效率。" 在计算机科学中，回溯法是一种重要的算法策略，尤其适用于解决那些具有多种可能性和约束条件的问题。当问题的解可以通过一系列决策或选择来构建时，回溯法能够有效地缩小搜索空间。与暴力法不同，回溯法不是盲目地遍历所有可能的解决方案，而是采用深度优先的方式探索问题状态树，并在每个节点处进行剪枝，即检查当前选择是否可行。如果发现当前选择无法导致有效解，算法会撤销这次选择，尝试其他路径，甚至回到之前的决策点重新选择。 N个皇后问题是一个经典的回溯法应用实例，它要求在N×N的棋盘上放置N个皇后，使得没有任何两个皇后能相互攻击（即不在同一行、同一列或同一对角线上）。使用暴力法，每行放置一个皇后，解的数量是N!；但如果允许任意放置，解的数量将呈指数级增长。相比之下，回溯法通过在每一步放置皇后时检查冲突并适时回溯，可以显著减少需要检查的解的数量，从而提高算法效率。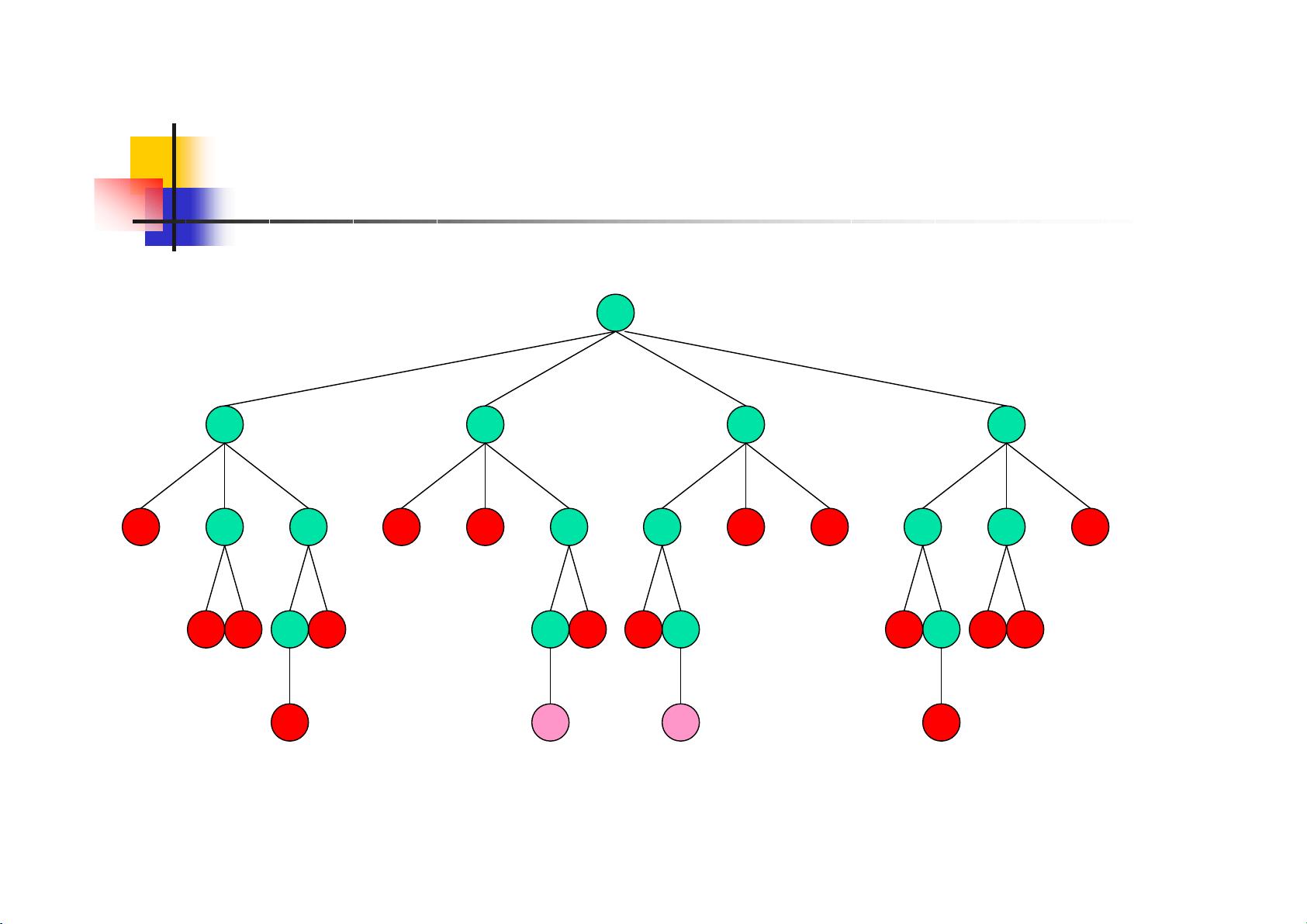 对于4个皇后的N-Queen问题，暴力法会生成4! = 24种排列，但回溯法通过在每一步判断冲突并回溯，可以更高效地找到所有有效的解。图示中展示了4-Queen问题的状态树，用回溯法可以更清晰地描绘出解决方案的路径，避免无效分支的扩展。 此外，回溯法还可应用于其他类型的问题，如子集求和问题（寻找集合中元素的特定子集使得其和等于目标值）、图着色问题（给图的各个顶点分配颜色，要求相邻顶点颜色不同）以及0/1背包问题（在容量有限的背包中选取物品以最大化价值，每个物品要么不选要么全选）。这些问题都具有大量的潜在解决方案，而回溯法提供了一种系统性的、高效的探索方法。 回溯法作为一种算法策略，通过深度优先搜索和剪枝策略，能够在复杂的问题空间中有效地寻找解。它适用于需要进行多步决策且每步都有约束的问题，通过即时验证和回溯，避免了无效的工作，提高了算法性能。