分支限界法详解：算法设计中的关键策略与应用

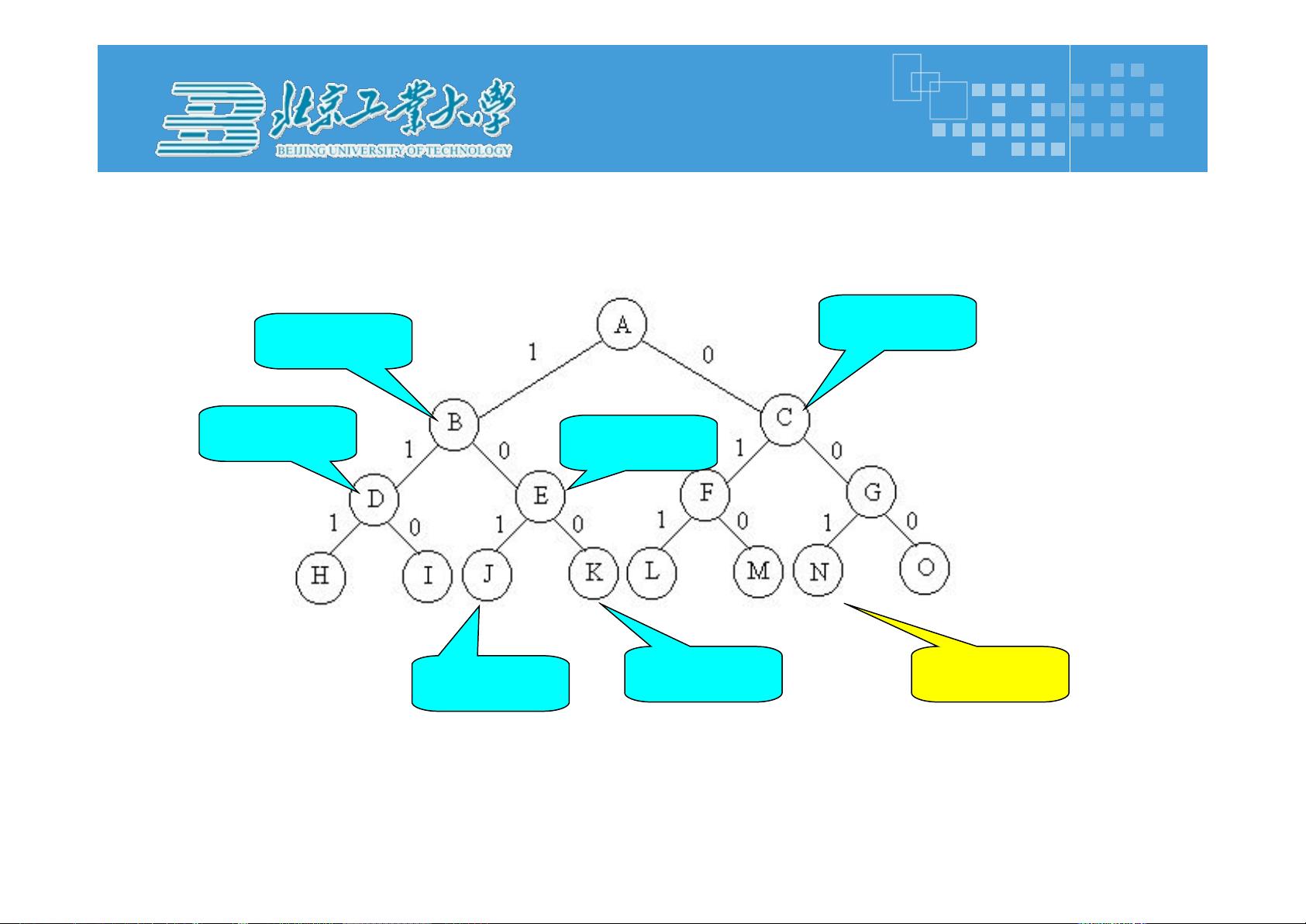
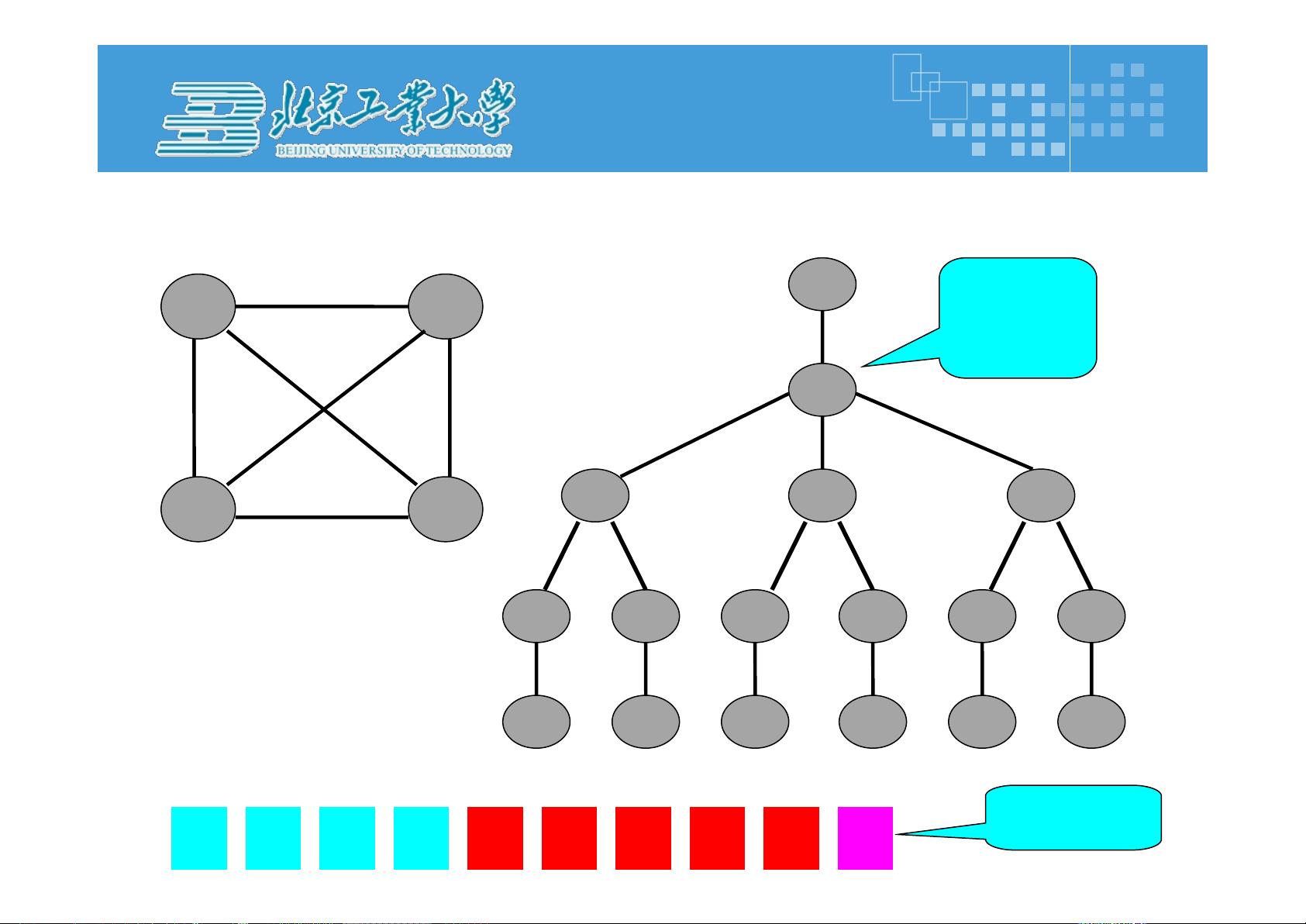
"《算法分析与设计》第六讲深入探讨了分支限界法这一核心概念。分支限界法是一种在求解优化问题时，有选择地进行搜索的策略，它在回溯法的基础上进行了改进，以避免盲目的搜索。该方法的核心在于剪枝操作，即在搜索过程中，通过计算每个结点的函数值（限界）来判断是否有必要进一步探索某个分支，从而减少无效的搜索。 首先，分支限界法的基本思想是区分于回溯法，后者可能穷举所有可能的解决方案，而分支限界法则更侧重于找到满足约束条件的最优解。它采用广度优先或最小耗费优先的方式搜索解空间树，确保在每个阶段都向着最有希望接近最优解的方向前进。 具体来说，分支限界法的执行步骤如下： 1. 扩展结点时，生成所有儿子结点，并从活结点表中根据限界函数值选择下一个最有潜力的结点作为扩展结点。 2. 活结点在扩展后，仅有一次成为扩展结点的机会，儿子结点根据是否可行或是否是最优解进行剪枝。非最优的结点被剔除，其余的加入活结点表。 3. 这个过程不断迭代，直至找到满足约束条件的解或者活结点表为空，搜索结束。 举例而言，分支限界法在多个经典问题中发挥作用，如单源最短路径问题、装载问题、0-1背包问题和货郎担问题等，这些问题都涉及到寻找在约束条件下最优的解决方案。 通过学习分支限界法，学生不仅能够理解其算法框架，包括队列式（FIFO）和优先队列式两种实现方式，还能掌握如何在实际问题中灵活运用，设计出高效的搜索策略。分支限界法是优化算法设计的重要工具，对于理解和解决复杂的优化问题具有重要意义。"