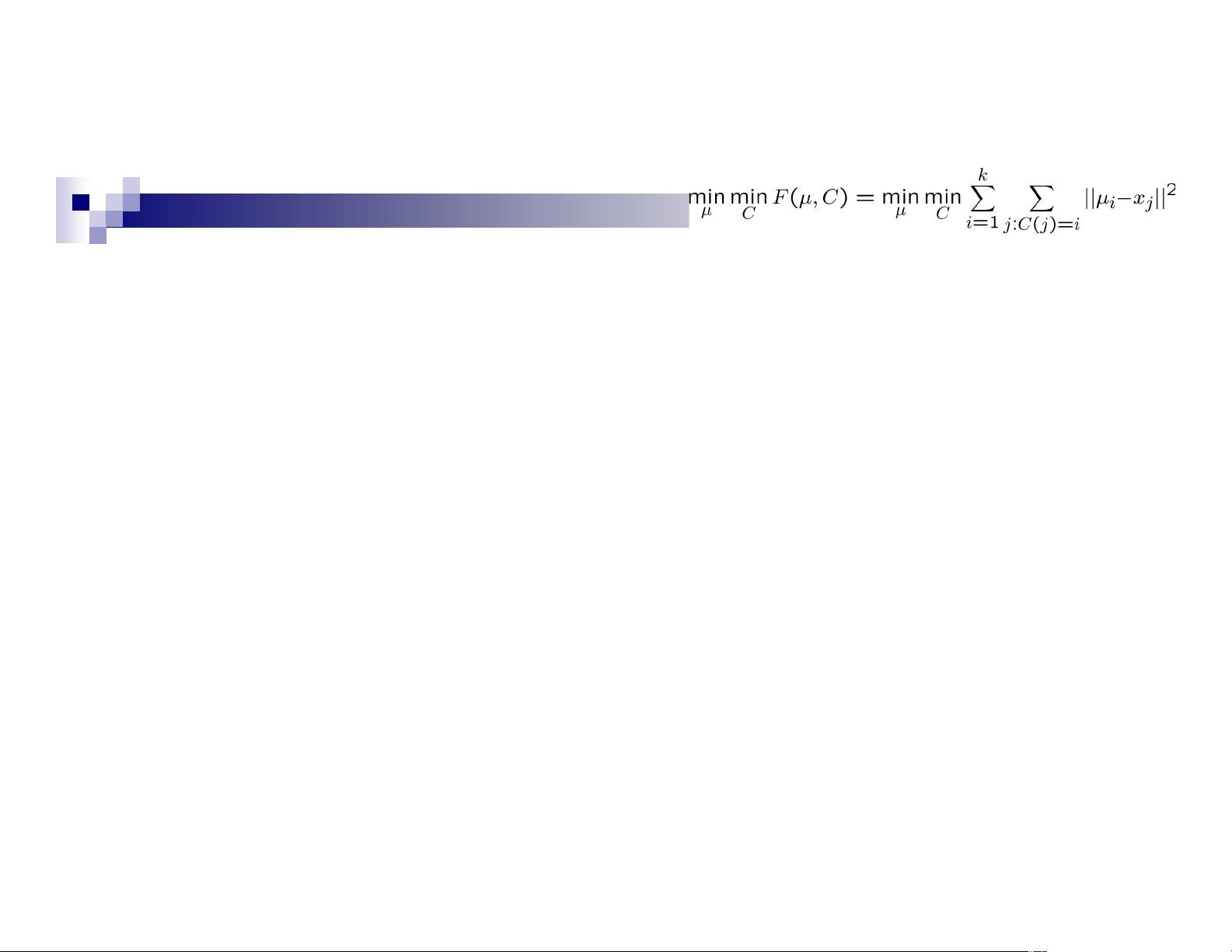理解K-means聚类算法

"k-means聚类讲解" k-means聚类是一种广泛应用的无监督学习算法，主要用于数据的分组或分类。它通过寻找数据集中自然存在的结构，将相似的数据点聚集到一起，形成所谓的“簇”（clusters）。在这个过程中，用户需要指定希望划分的簇的数量（k值）。 在k-means算法的执行流程中，首先，用户需要确定希望得到的聚类个数。例如，如果用户想要将数据分为5个簇，那么k就等于5。然后，算法会随机初始化k个聚类中心。这个初始位置的选择对最终结果有直接影响，因为不同的起始点可能会导致不同的聚类结果。随机性是k-means算法的一个重要特征，可能会导致多次运行得到不同的结果。 接下来，算法进入迭代阶段。对于每个数据点，算法计算其与所有聚类中心的距离，并将其分配到最近的中心所在的簇。这一过程反映了数据点的“归属”，即每个数据点被归类到与其距离最近的簇中心的簇中。随着聚类过程的进行，每个中心“拥有”了一组与之关联的数据点。 在数据点分配完成之后，算法会计算每个簇的质心，也就是中心点。质心通常是簇内所有数据点的几何中心，即各个坐标维度上的平均值。更新后的质心会替代原来的聚类中心，这个过程会持续进行，直到聚类中心的位置不再显著变化，或者达到预设的迭代次数上限，此时算法停止，最终的聚类结果产生。 k-means算法的优点在于它的简单性和效率，尤其是在处理大规模数据集时。然而，它也有一些局限性：首先，它对初始聚类中心的选择敏感，可能导致局部最优解；其次，它假设数据分布是凸的，且簇的大小相近，这在实际问题中可能不成立；最后，k-means无法处理非凸形状的簇和不同大小的簇。 Gaussian混合模型（Gaussian Mixture Models, GMM）是另一种常用于聚类的方法，它可以更好地处理复杂的概率分布，包括多模态分布。GMM通过组合多个高斯分布来建模数据，每个聚类对应一个高斯分布，使得模型能够适应更复杂的数据结构。 总结来说，k-means聚类是一种基本的无监督学习方法，适用于发现数据的分组结构，而GMM则提供了更灵活的概率模型来处理数据聚类。理解这两种方法的原理和适用场景，对于数据科学家和机器学习工程师来说至关重要。