理解SM2算法：椭圆曲线加密原理

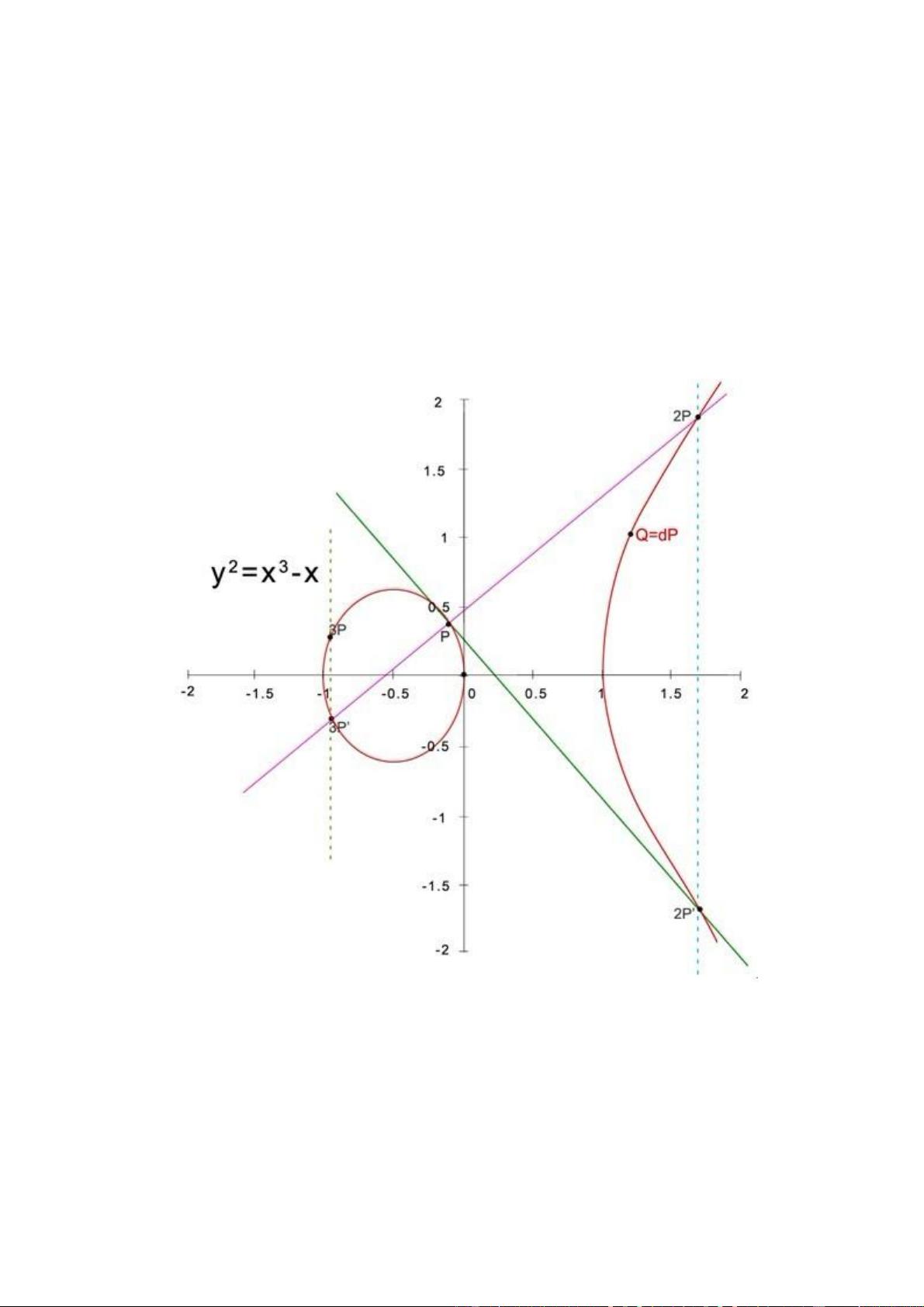
"本文主要介绍了SM2算法的基本原理和流程，包括椭圆曲线算法的数学基础，SM2算法的系统参数，以及密钥对的生成和加密过程。SM2算法是一种基于椭圆曲线密码学（ECC）的公钥加密算法，是中国国密标准的一部分，用于确保数据的安全传输和存储。" 1. **SM2算法原理** SM2算法基于椭圆曲线密码学，其核心是椭圆曲线方程`y^2 = x^3 + ax + b`。在这个特定的数学结构上，可以通过点的倍增操作来生成公钥和私钥。私钥`d`是一个秘密的整数，而公钥`P`是通过将私钥乘以基点`G`得到的点 `(xP, yP)`。 2. **椭圆曲线系统参数** - **域的规模**: q=p，其中p是一个大于3的素数，形成有限域Fp。 - **SEED**: 可选的随机种子，用于生成其他参数，长度至少192位。 - **曲线方程**: 椭圆曲线E的定义，`y^2 = x^3 + ax + b`，其中a和b是Fp中的元素。 - **基点G**: 曲线上一个非无穷远点，具有阶n，满足`n > 2 * 191`且`n > 4 * p1 = 2`。 - **余因子h**: #E(Fp) = n，即曲线E在Fp上的点的数量除以n。 3. **密钥对生成** - 输入: Fq上的有效椭圆曲线系统参数集合。 - 输出: 一个与系统参数相关的密钥对`(d; P)`，其中d是私钥，P是公钥。 - 步骤: a. 生成随机整数d，范围在`[1, n-2]`。 b. 计算点P = [d]G，即基点G的d倍点。 c. 密钥对由d和P组成。 4. **加密算法** - 加密消息M的步骤: A1. 生成随机数k，范围在`[1, n-1]`。 A2. 计算点C1 = [k]G，并将点数据转换为比特串。 A3. 计算S = [h]PB，如果S是无穷远点则报错。 A4. 计算[k]PB，将坐标转换为比特串。 A5. 使用KDF（Key Derivation Function）函数从坐标数据中提取密钥t，长度为klen位。 SM2算法的加密机制确保了即使知道公钥P，也无法轻易地推导出私钥d，从而保证了通信的安全性。这种加密方式相比传统的RSA等算法，具有更高的安全性，同时在同等安全级别下，密钥长度更短，计算效率更高。因此，SM2算法被广泛应用于中国的加密标准，特别是在金融、政府、物联网等领域。