稀疏约束与噪声群测试快速分裂算法研究
版权申诉
51 浏览量
更新于2024-07-06
收藏 784KB PDF 举报
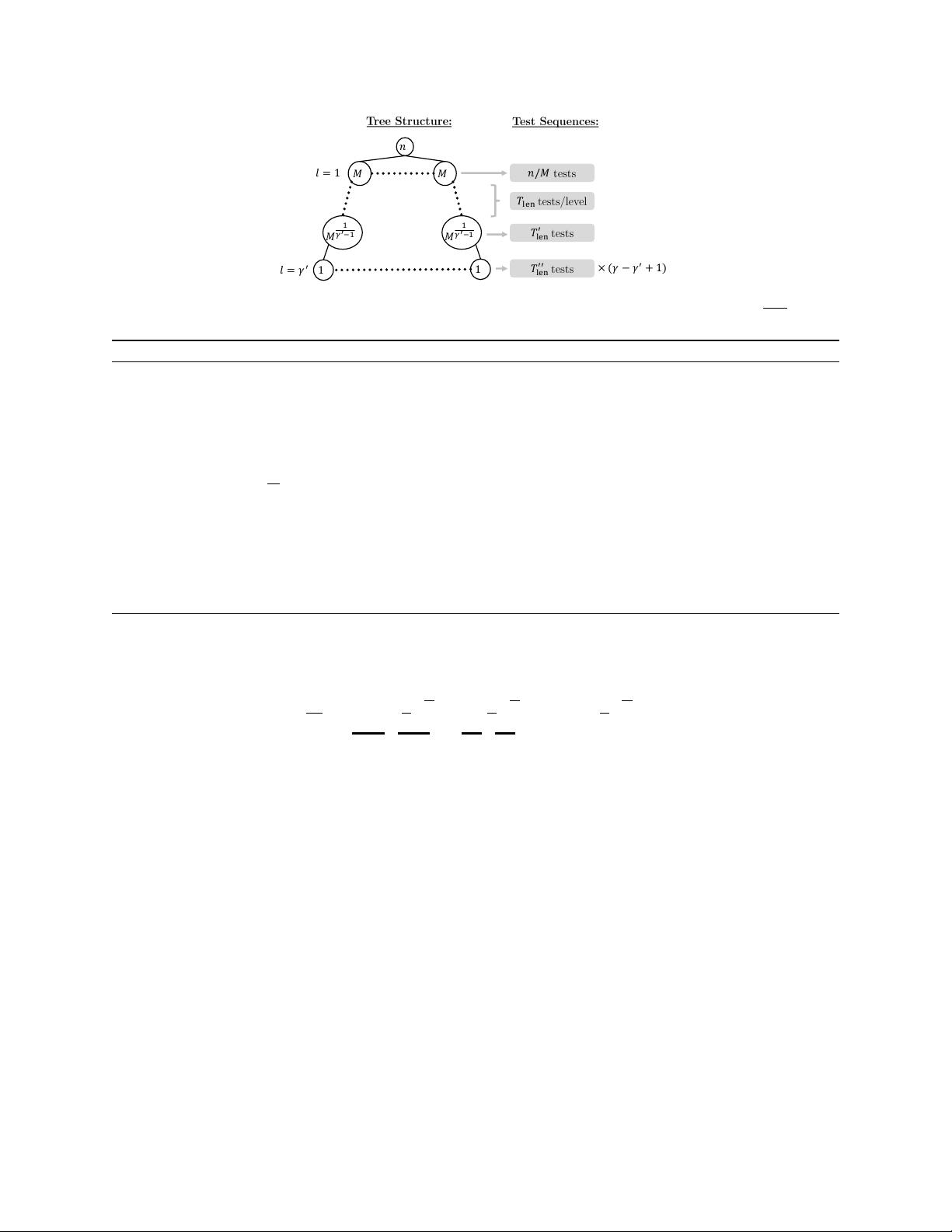
"这篇文档是关于稀疏约束和噪声群测试的快速分裂算法的研究,由Eric Price, Jonathan Scarlett和Nelvin Tan共同撰写。该研究关注的是在大规模物品集合中,通过测试找出缺陷子集的问题,该问题在医疗检测、DNA测序、通信协议等领域有广泛应用。文章探讨了两种限制条件下的问题:一是物品可有限分割,每个物品最多参与γ个测试;二是测试规模受限,每个测试最多合并ρ个物品。此外,还考虑了存在错误概率的噪声测试结果情况。对于这两种设定,作者提出了一种快速分裂算法,并证明了其在测试数量和解码时间上的近似最优性,尤其是在错误概率趋于零的情况下。"
本文的核心知识点包括:
1. **群组测试(Group Testing)**:这是一种识别大量物品中缺陷子集的优化策略,通过设计测试来确定至少有一个缺陷物品的组。这种方法在实际应用中可以大大减少测试次数。
2. **稀疏约束**:文章讨论了两种稀疏约束形式。第一种是物品可有限分割,即每个物品最多能参与γ次测试,这限制了测试的复杂度。第二种是测试规模约束,每个测试只能合并不超过ρ个物品,这影响了测试设计的灵活性。
3. **噪声模型**:引入了测试结果可能出现错误的噪声模型,每个测试结果独立地以一定的概率翻转,这使得问题更具挑战性,需要算法具备抗干扰能力。
4. **快速分裂算法**:为了应对上述挑战,作者提出了一种快速分裂算法,它能够在保证错误概率逐渐减小的前提下,有效地进行缺陷物品的识别。
5. **性能分析**:该算法不仅在所需的测试数量上具有近似最优性,而且在解码时间上也表现出优良的效率,这意味着它在处理大规模数据时能够高效运行。
6. **恢复保证**:论文关注的是“对于-each”恢复保证,意味着算法可以以渐近于零的错误概率逐个正确恢复缺陷物品。
7. **应用背景**:群组测试的理论研究对实际场景有直接指导意义,如医疗诊断中的大规模筛查、DNA序列分析中的缺陷定位以及通信系统中的错误检测等。
8. **理论贡献**:该研究提供了在噪声环境下处理稀疏约束群组测试问题的新方法,对优化大规模数据处理策略具有重要意义。
这篇文章深入研究了在有约束条件和噪声存在的群组测试问题,并提出了一种新的快速分裂算法,该算法在理论和实践层面上都有重要价值。
点击了解资源详情
131 浏览量
点击了解资源详情
2022-02-09 上传
2022-01-17 上传
2021-03-10 上传
2021-08-22 上传
2022-02-08 上传
145 浏览量

易小侠
- 粉丝: 6634
- 资源: 9万+
最新资源
- Risk Assessment Guidebook for e-Commerce/e-Government
- GDB调式ARM开发板
- Exchange Server 2007快速部署指南
- 工业电器现行国标大全
- LoadRunner使用手册.pdf
- 模拟系统使用说明.doc
- Hibernate开发指南
- 深入Spring 2:轻量级J2EE开发框架原理与实践 .pdf
- 使用TEFS(TM)平台构建应用系统
- bht8000开发手册
- Oracle数据库维护.pdf
- Oracle的入门心得.pdf
- Apache 2.2 中文手册.pdf
- java swing架构--中英文对照版
- REALBASIC开发指南
- arcgis server详细安装部署文档