ANSYS在有限元分析中的理论与应用详解

1星需积分: 9 151 浏览量更新于2024-08-02 1 收藏 13.47MB PDF 举报

《有限元分析：ANSYS理论与应用》是由Saeed Moaveni撰写的一本经典著作，专为那些希望深入理解有限元分析（Finite Element Analysis, FEA）理论及其在ANSYS软件中的实际应用的读者而设计。本书由Minnesota State University, Mankato的作者以其丰富的学术背景和教学经验为基础，结合Prentice Hall出版社的出版支持，提供了全面的教育资源。有限元方法是工程领域中的核心分析工具，它将复杂的物理问题转化为可解决的离散数学模型。在书中，Moaveni教授阐述了有限元的基本概念，如基本原理、网格划分技术、节点和元素的定义，以及如何通过这些元素来模拟连续物理现象，如结构力学、热传导和流体动力学等。ANSYS是一个广泛使用的商业软件平台，它提供了强大的FEA工具集，本书详尽地介绍了如何利用ANSYS进行求解、模型验证、结果解释和后处理。章节内容涵盖了FEA的各个方面，包括基本理论、线性与非线性分析、动态分析、接触和边界条件处理，以及材料行为和几何非线性的考虑。此外，书中还包含了针对不同行业应用的实际案例，帮助读者将理论知识与实践相结合。读者可以借此书学习到如何创建、验证和优化模型，以及如何解读和报告分析结果。书中的参考资料和索引进一步扩展了学习范围，确保读者能够追踪到更深层次的理论研究和最新发展。此外，该书的编排和设计便于理解和学习，包括清晰的示例、实用的步骤和提示，使得即使是初学者也能逐步掌握有限元分析的复杂概念。总结来说，《有限元分析：ANSYS理论与应用》是一本不可或缺的参考书籍，不仅适合大学学生和研究人员深化对有限元理论的理解，也适合工程师、设计师和其他专业人士提升其在工程设计和项目实施中的FEA技能。通过阅读这本书，读者不仅能掌握理论知识，还能学会如何高效地运用ANSYS这一强大工具解决实际工程问题。

Chapter

Introduction

Section 1.5 Direct Formulation

The final global stiffness matrix is obtained by assembling, or adding, together

each element's position in the global stiffness matrix:

Note that the global stiffness matrix obtained using elemental description, as given by

Eq.

(1.16),

identical to the global stiffness matrix we obtained earlier from the analy-

sis of the free body diagrams of the nodqas given by the left hand side of Eq. (1.10).

Apply boundary conditions and loads.

The bar is fixed at the top, which leads to the boundary condition u,

O.The ex-

ternal load

is applied at node 5. Applying these conditions results in the fol-

lowing set of linear equations.

Again, note that the first row of the matrix in Eq. (1.17) must contain a 1 followed

by four

0's to read

0, the given boundary condition. Also note that in solid

mechanics problems, the finite element formulation will always lead to the fol-

lowing general form:

[stiffness matrix]{displacement matrix]

{load matrix]

Solution

Phase

Solve a system of algebraic equations simultaneously.

In order to obtain numerical values of the nodal displacements, let us assume that

10.4

lo6 lb/in2 (aluminum),

2 in,

in,

0.125 in,

10 in,

and

1000 Ib. You may consult Table 1.4 while working toward the solution.

TABLE

1.4

Properties of the elements in Example 1.1

Average Modulus

cross-sectional Length elasticity

Element Nodes area (in2) (in) (Ib/in2)

1 12 0.234375

2.5 10.4

lo6

2 2 3 0.203125 2.5 10.4

106

4 0.171875

2.5 10.4

106

4 5 0.140625 2.5 10.4

106

Element's stiffness

coefficient

(Ib/in)

975

10'

845

10'

715

10'

585

10'

'Ihe variation of the cross-sectional area of the bar in the y-direction can be

expressed by:

Using Eq. (1.18), we can compute the cross-sectional areas at each node:

0.25 in2

0.25

0.0125(2.5)

0.21875 in2

Next, the equivalent stiffness coefficient for each element is computed from the

equations

(Ai+l

Ai)E

ke,

and the elemental matrices are

Assembling the elemental matrices leads to the generation of the global stiffness

matrix:

975

-975 0 0

-975 975

845 -845 0

-845 845

715 -715

0 0

-715

715

585 -585

0 0

0 -585

585

Chapter

Introduction

{reaction matrix)

[stiffness

matrix]{displacement matrix)

{load matrix)

Because Example

1.1

is a simple problem, we do not actually need to go through

the matrix operations

the aforementioned general equation to compute the re-

action forces. However,

a demonstration, the procedure is shown here. From the

general equation, we get

975 -975 0 0 0 0

where

R1,

R2,

R4,

and

represent the reactions forces at nodes

through 5,

respectively. Performing the matrix operation, we have

The negative value of

simply means that the direction of the reaction force is

up (because we assumed that the positive y-direction points down). Of course, as

expected, the outcome is the same as in our earlier calculations because the rows

of the above matrix represent the static equilibrium conditions at each node. Next,

we will consider finite element formulation of a heat transfer problem.

EXAMPLE 1.2

typical exterior frame wall (made up of 2

studs) of a house contains the materi-

als shown in the table below. Let us assume an inside room temperature of 70°F and an

outside

air

temperature of 20°F, with an exposed area of 150 ft2. We are interested in de-

termining the temperature distribution through the wall.

Items

Resistance U-factor

hr~f&FIBtu Btdhr.ft2.F

Outside film resistance (winter, 15-mph wind) 0.17

5.88

2. Siding, wood (112

lapped)

0.81 1.23

3. Sheathing

(112 in regular) 1.32 0.76

Insulation hatt (3

3112 in)

11.0 0.091

Gypsum wall board

(112

in)

0.45 2.22

6. Inside film resistance (winter)

0.68

1.47

Section

1.5

Direct Formulation

FIGURE

1.7 Finite element

model

of Example 1.2.

Preprocessing Phase

Discretize the solution domain into finite elements.

We will represent this problem by a model that has seven nodes and six elements,

as shown in Figure 1.7.

Assume a solution that approximates the behavior of an element.

For Example 1.2, there are two modes of heat transfer (conduction and convection)

that we must first understand before we can proceed with formulating the con-

ductance matrix and the thermal load matrix. The steady state thermal behavior

of the elements

(2), (3),

(4),

and (5) may be modeled using Fourier's Law. When

there exists a temperature gradient in a medium, conduction heat transfer occurs,

as shown in Figure

1.8.

The energy is transported from the high-temperature re-

gion to the l~w~tem~erature region by molecular activities.The heat transfer rate

is given by Fourier's Law:

is the X-component of the heat transfer rate,

the thermal conductivity of the

medium,

is the area, and

is the temperature gradient. The minus sign in

FIGURE

1.8

Heat transfer in a medium by

conduction.

Chapter

Introduction

Eq. (1.21) is due to the fact that heat flows in the direction of decreasing temper-

ature. Equation (1.21) can be written in a difference form in terms of the spacing

between the nodes (length of the element)

and the respective temperatures of

the nodes

and

1, Ti and Ti+,

according to the equation

In the field of heat transfer, it is also common to write Eq. (1.22) in terms of

the thermal transmittance coefficient U, or, as it is often called, the U-factor

4).

The U-factor represents thermal transmission through a unit area and

has the units of Btu/hr.ft2-F. It is the reciprocal of thermal resistance. So,

UA(T,+l

Ti)

(1.23)

The steady state thermal behavior of elements (1) and

(6)

may be modeled

using Newton's Law of Cooling. Convection heat transfer occurs when a fluid in

motion comes into contact with a surface whose temperature differs from the mov-

ing

fluid.The overall heat transfer rate between the fluid and the surface is gov-

erned by Newton's Law of Cooling, according to the equation

hA(T,

Tf)

(1.24)

where h is the heat transfer coefficient, T, is the surface temperature, and Tf rep-

resents the temperature of the moving fluid.Newton's Law of Cooling can also be

written in terms of the U-factor, such that

UA(T,

Tf)

(1.25)

where U

h, and it represents the reciprocal of thermal resistance due to con-

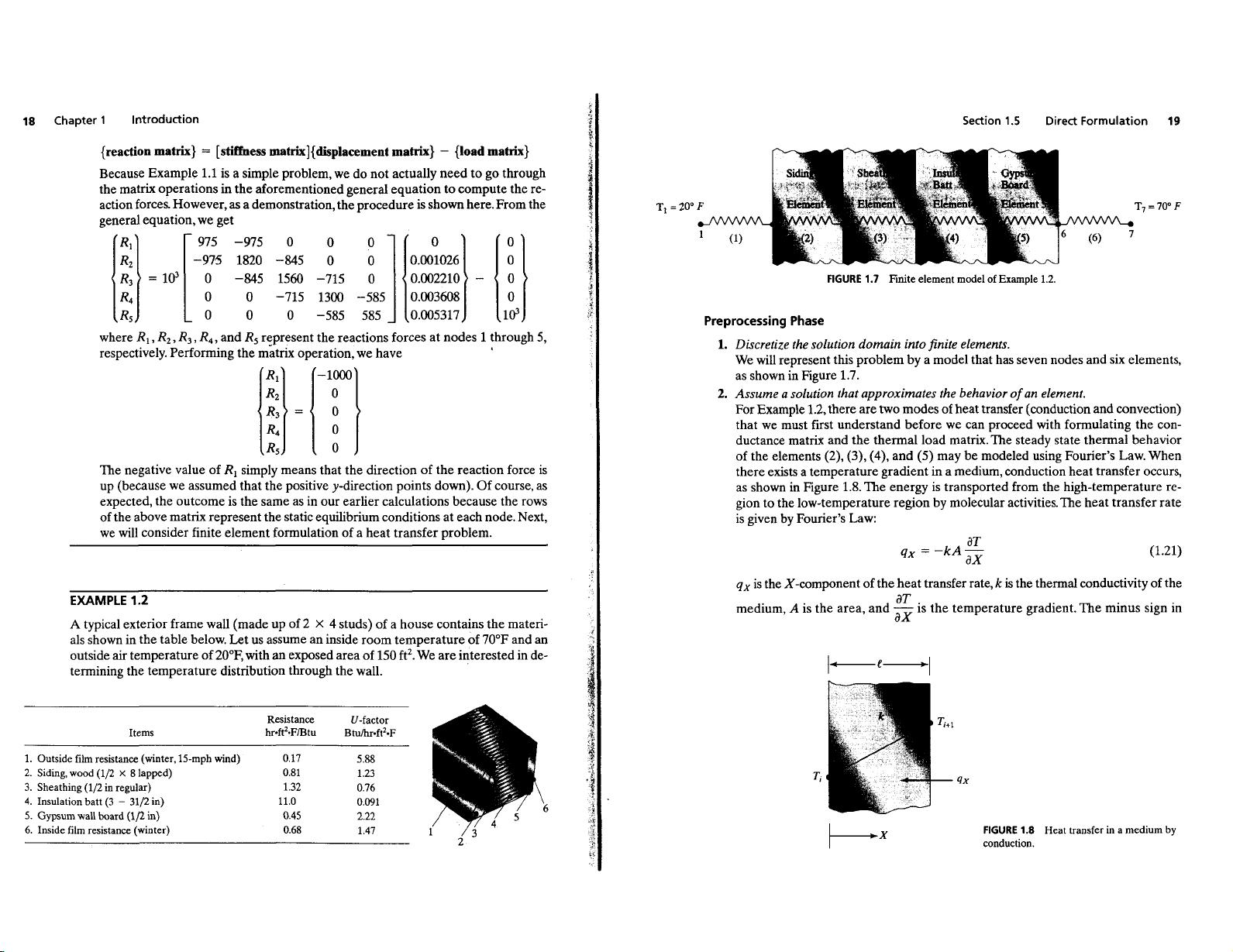
vection boundary conditions. Under steady state conduction, the application of

energy balance to a surface requires that the energy transferred to this surface via

conduction must be equal to the energy transfer by convection. This principle,

is depicted in Figure 1.9.

FIGURE

1.9

Energy

balance at a

surface

with a convective heat transfer.

Section

1.5

Direct Formulation

Now that we understand the two modes of heat transfer involved in this

problem, we can apply the energy balance to the various surfaces of the wall, start-

ing with the wall's exterior surface located at node 2. The heat loss through the

wall due to conduction must equal the heat loss to the surrounding cold air by

convection. That is,

U2A(T3

T2)

Ul A(T2

TI)

The application of energy balance to surfaces located at nodes

3,4,

and

yields the

equations

U3A(T4

T3)

U2A(T3

T2)

U4A(T5

T4)

U3A(T4

T3)

U5 A(T6

T5)

U4A(T5

T4)

For the interior surface of the wall, located at node

the heat loss by convection

of warm air is equal to the heat transfer by conduction through the gypsum board,

according to the equation

Separating the known temperatures from the unknown temperatures, we have:

+(Ul

U2)AT2 -U2 AT,

Ul AT,

-U2AT2 +(U2+U3)AT3 -U3AT4

-U3AT3 +(U3

U4)AT4 -U4AT5

-U4AT4 +(U4+U5)AT5 -U5AT6

-U5 AT5 +(Us

U6)AT6

U6AT,

The above relationships can be represented in matrix form as

Note that the relationship given by Eq. (1.27) was developed by applying the con-

servation of energy to the surfaces located at nodes 2,3,4,5, and

Next, we

will

con-

sider the elemental formulation of this problem, which

will

lead to the same results

Develop equations for

element.

general, for conduction problems, the heat transfer rates, q, and q,, ,and the nodal

temperatures, Ti and Ti+,

for an element are related according to the equations

剩余271页未读，继续阅读

tangtangtoy

粉丝: 2
资源: 6

ANSYS在有限元分析中的理论与应用详解

Finite Element Analysis Theory and Applications with ANSYS - Saeed Moaveni

Finite Element Simulations with ANSYS Workbench 14 by HH Lee

Finite Element Analysis Theory and Application with ANSYS, 3rd Edition

San Le's Free Finite Element Analysis-开源

Finite-ELement-Analysis-Nap:结构分析-matlab开发

Finite Element Method - Fluid Dynamics - Zienkiewicz and Taylor

Finite-Temperature Field Theory-Principles and Applications

Finite Element Method - Fluid Dynamics - Zienkwicz and Taylor.pdf

A First Course In The Finite Element --- by Daryl Logan

Non-linear 3D Finite Element Solver:Non-linear 3D Finite Element Solver-matlab开发

最新资源