L1-范数非局部总变分Retinex模型在图像恢复中的高效应用

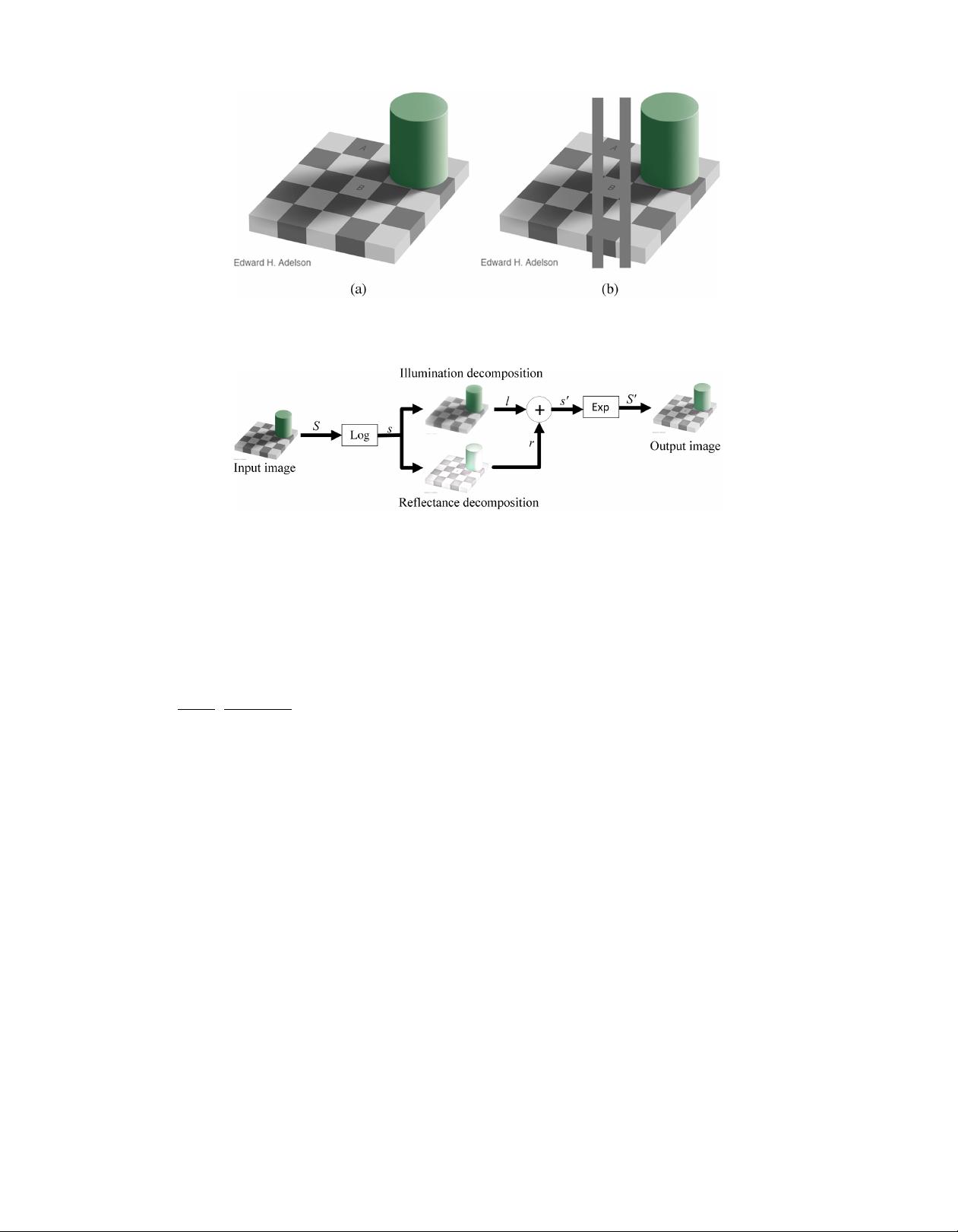
"这篇研究论文提出了一种高效的基于L-1范数的Retinex非局部总变分模型，用于图像恢复。该模型利用非局部微分算子在图像处理中保留图像特性，如平滑度、边缘和纹理。通过Retinex理论建立了一个L-1范数的非局部总变分（NLTV-L1）模型，并采用交替方向乘子法（ADMM）的快速计算算法求解。实验结果表明，NLTV-L1方法在图像恢复方面表现出色，能更好地保持图像质量并增强细节。" 本文主要探讨了图像恢复领域的一种新方法，即基于L-1范数的Retinex非局部总变分模型。Retinex理论是图像处理中的一个基础概念，它模拟了人类视觉系统对图像亮度和颜色的感知，旨在分离图像的照明和反射部分，以提高图像的质量。非局部总变分（Non-local Total Variation，NLTV）则是Retinex理论的一个扩展，它考虑了图像中像素之间的相似性，而非仅关注局部邻域，这样可以更好地保持图像的全局特性。 在传统的Retinex模型中，通常使用L-2范数来度量图像的变化，但L-2范数可能会导致过度平滑，丢失图像细节。因此，该研究提出了使用L-1范数，它对噪声更具有鲁棒性，能更好地保持图像的边缘和纹理信息。L-1范数的引入使得模型在处理图像恢复时，尤其是在去除噪声和恢复细节方面，具有更好的性能。 论文中提到的快速计算算法是交替方向乘子法（Alternating Direction Method of Multipliers，ADMM），这是一种优化工具，常用于解决包含拉格朗日乘子的变分问题。ADMM的优势在于它可以将复杂问题分解为更易于管理的子问题，从而提高求解效率。在NLTV-L1模型中，ADMM被用来有效地求解非局部总变分问题，降低了计算复杂度，提高了算法的执行速度。 通过实验证明，基于NLTV-L1的Retinex模型在图像恢复任务上表现出色，不仅能够有效去除噪声，还能保持图像的结构和细节，相比于传统方法，其恢复效果更为理想。这一成果对于图像处理领域的研究和应用具有重要意义，特别是在高清晰度图像恢复、低光照图像增强以及图像去噪等方面有着广泛的应用前景。