机器学习入门：解析神经网络与曲线拟合

"本文介绍了机器学习中的基础概念，特别是神经网络和回归问题的解析，通过实例讲解了曲线拟合和梯度下降法的工作原理。" 在机器学习领域，神经网络是一种模仿人脑神经元结构的计算模型，用于识别复杂的模式和规律。当我们谈论“机器学习入门——浅谈神经网络”时，首先需要理解的是基础的回归问题。回归是机器学习中的一种基本任务，主要涉及预测连续变量的值，如预测房价、股票价格等。在这个过程中，机器需要学习如何从输入数据中提取特征，并基于这些特征进行预测。 文章提到了一个例子，通过一串数字来说明回归问题。第一串数字1、3、5、7、9、11，机器很容易发现这是一个简单的奇数序列，而第二串数字0.14、0.57、1.29、2.29、3.57、5.14则需要通过曲线拟合来找出规律。曲线拟合是回归问题的一个解决方案，它尝试找到一条最佳拟合曲线，使得所有样本点到该曲线的平均距离最小。 在这个过程中，文章介绍了梯度下降法，这是优化算法的一种，广泛应用于神经网络的训练中。梯度下降法的目标是找到一组参数（在这个例子中是直线的斜率k和截距b），使得损失函数（误差之和）达到最小。在训练过程中，算法会不断地调整这些参数，使得损失函数的梯度（即损失函数的局部变化率）朝着负梯度方向下降，从而逐步接近全局最小值。一旦误差达到预设的阈值，或者梯度变得非常小，算法就认为找到了最佳参数，此时模型的预测效果最优。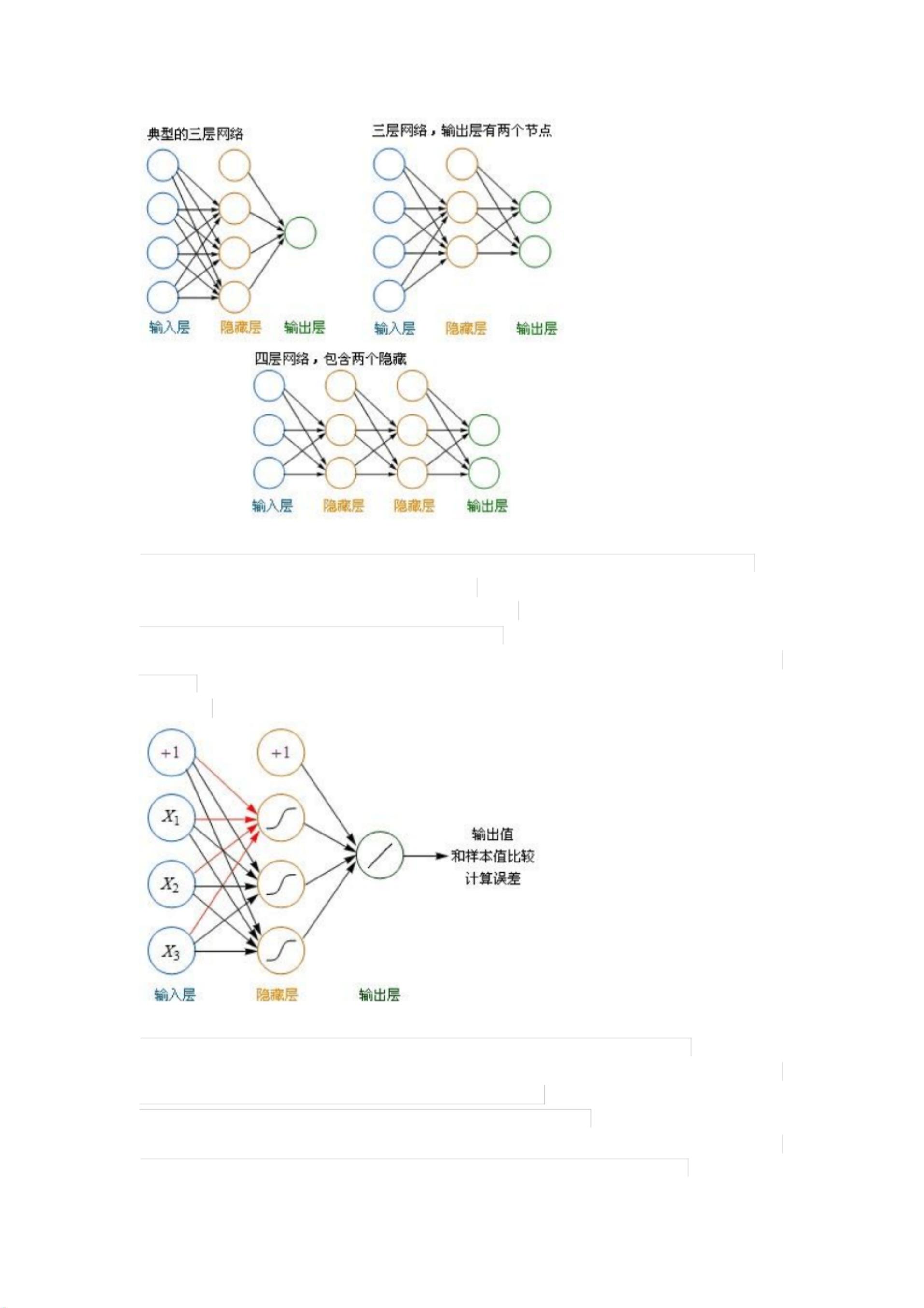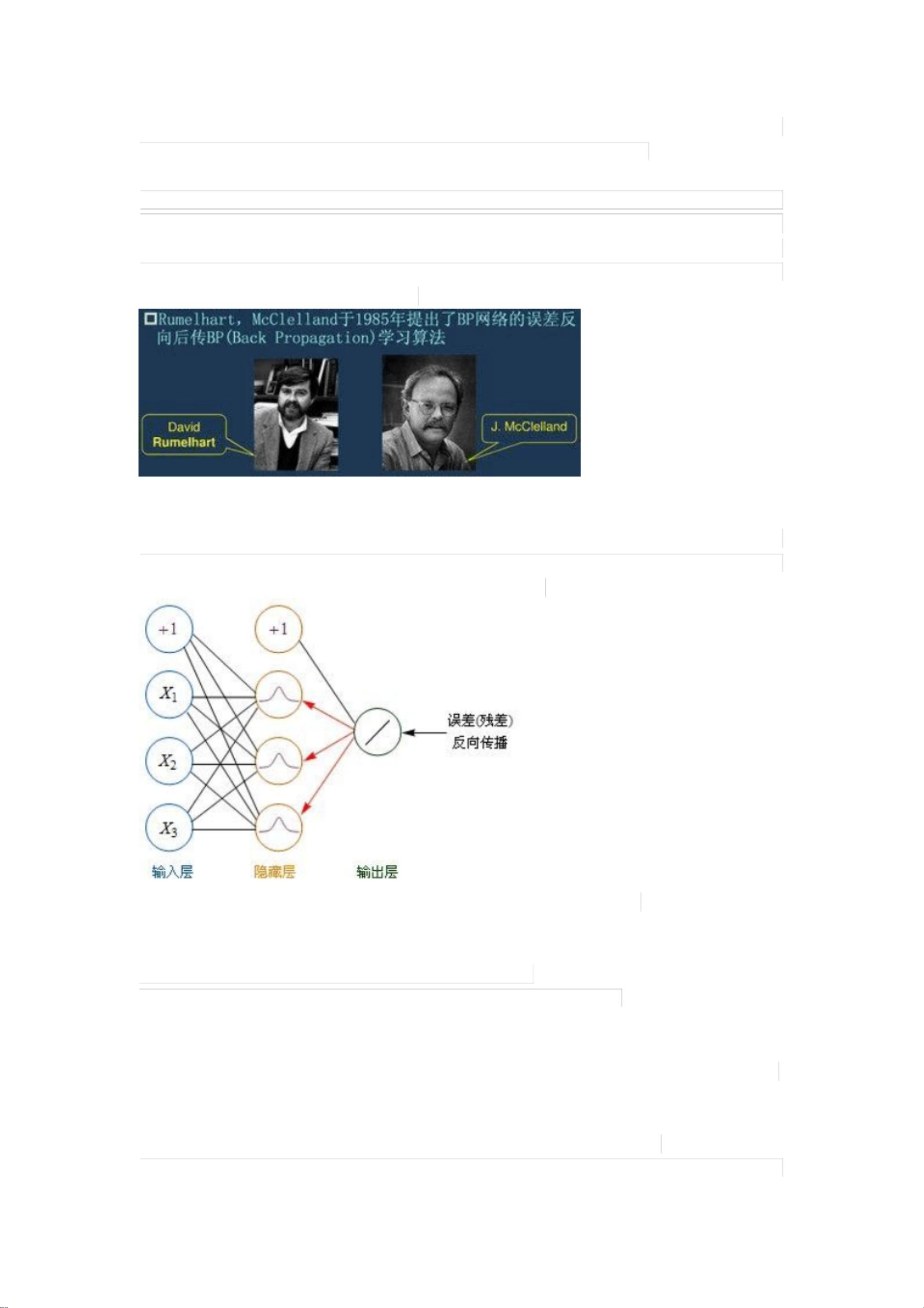 在神经网络中，除了简单的线性回归，还有更复杂的多层神经网络，其中包含许多隐藏层和激活函数。这些隐藏层可以学习到非线性的关系，使得神经网络能够处理更为复杂的任务。例如，卷积神经网络（CNN）擅长图像识别，循环神经网络（RNN）适用于序列数据如文本和音频。在训练神经网络时，通常会使用反向传播算法，结合梯度下降法更新权重，以最小化预测结果与真实值之间的差距。 这篇资料是机器学习初学者理解回归问题、曲线拟合和梯度下降法的良好起点。掌握这些基础知识对于后续深入学习神经网络和深度学习至关重要，因为这些概念构成了现代人工智能技术的基础。通过实践和理论的结合，读者可以逐步构建自己的机器学习模型，解决实际问题。