多元函数积分学1：极坐标作图与极限计算详解

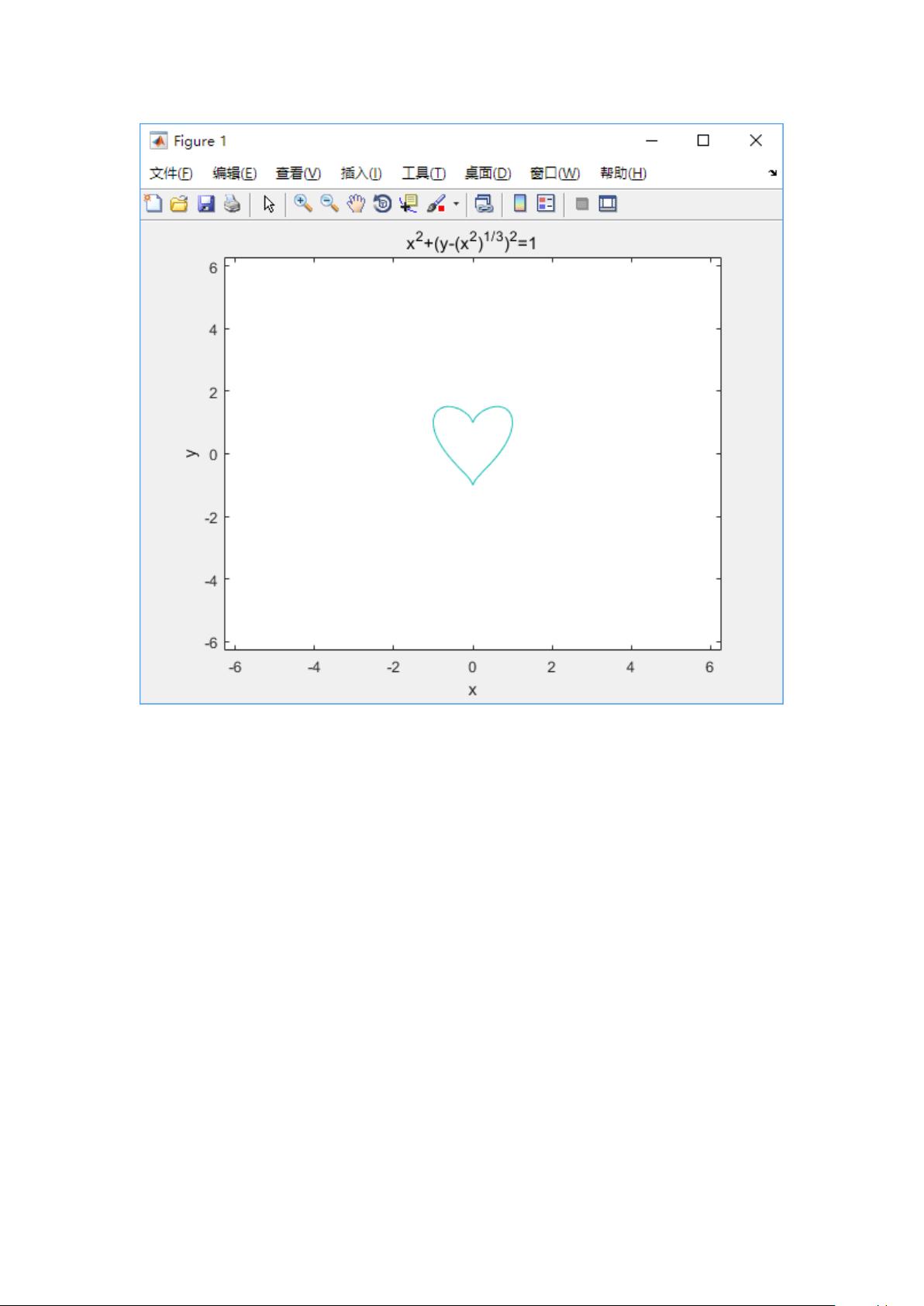
工数上机作业答案1；八、多元函数积分学1、>> syms r t;;一：一元函数作图1,ezpolar('3*cos(3*(theta)) ',[0,2*pi])2, ezpolar('3*sin(2*(theta))',[0,2*pi]) 3, ezplot('2*(t sin(t))','2*((cos(t))-1)',[0,2*pi]) 4, ezplot('(x^2)*(y^2)=(y 1)^2*(4-y^2)',[-10,10]) 5． ezplot('x^2 (y-(x^2)^(1/3))^2=1') 二：极限的计算1，syms x;>> limit(sin(sin(x))/x-1,x,0) ans=02，syms n;>> limit(tan(pi/4 1/n)^n,n,inf)ans=exp(2)3，syms x;>> limit(x*(pi/2-asin(x/(sqrt(x*x 1)))),x,inf)ans=14(1) syms x;>> limit(1/(1 exp(1/(x-1))),x,1,'left') ans=1(2) syms x;>> limit(1/(1 exp(1/(x-1))),x,1,'right; 本文总结了工数上机作业答案1中的内容，主要包括多元函数积分学和一元函数作图，以及极限的计算。在多元函数积分学部分，通过数学符号运算来实现对一元函数的作图，包括绘制3*cos(3*(theta))、3*sin(2*(theta))以及2*(t*sin(t))等图像。而在极限的计算部分，使用syms进行变量的定义和limit函数进行数学极限的计算，包括sin(sin(x))/x-1、tan(pi/4 - 1/n)^n以及x*(pi/2-asin(x/(sqrt(x*x-1)))等极限的运算。 通过这些练习，可以帮助学生巩固多元函数积分学和一元函数作图的基本概念，同时加强对极限计算的理解和运用。这些内容不仅是数学课程中的重要知识点，也是培养学生逻辑思维和数学推理能力的重要手段。因此，建议学生在学习过程中，要对这些内容进行认真总结和练习，以便更好地掌握相关知识。