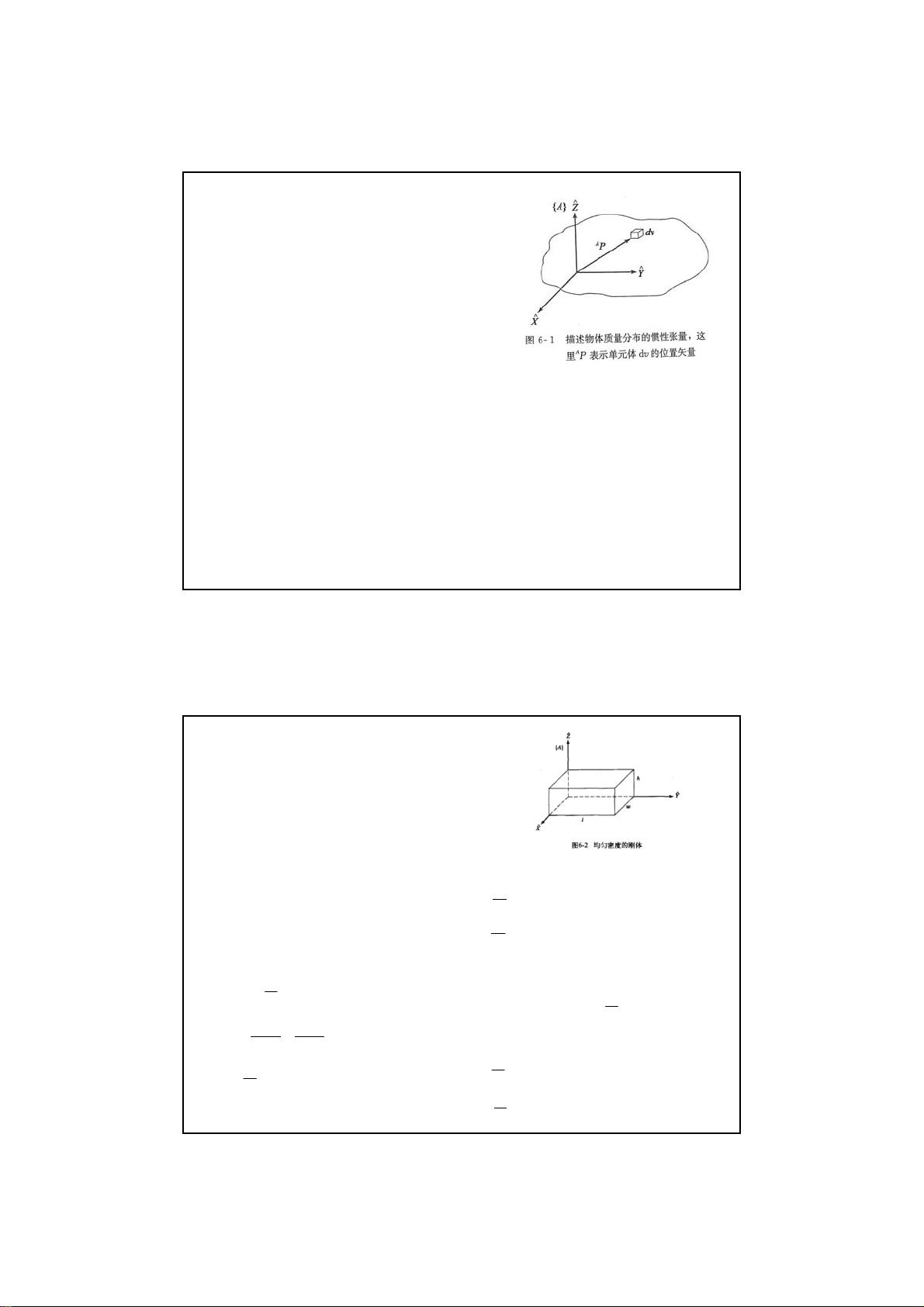
操作臂动力学解析：从牛顿-欧拉到拉格朗日方程

"本章深入探讨了操作臂的动力学，包括刚体的加速度、质量分布、牛顿方程和欧拉方程，以及动力学方程的迭代和封闭形式。重点介绍了拉格朗日公式在操作臂动力学中的应用，并讨论了如何建立笛卡尔空间的规范化动力学方程，同时考虑非刚体效应和动力学仿真。" 在《第6章-操作臂动力学》中，主要关注的是机器人操作臂在运动过程中所涉及的动力学原理和计算方法。首先，章节概述指出，之前的研究主要集中于操作臂的运动学，如静态位置、力和速度，但并未涉及产生这些运动所需的力量。本章的目标是确定关节驱动器所需的电机功率，解决伺服驱动系统的力控问题，以及通过动力学方程预测关节力矩和操作臂的运动。 研究方法分为拉格朗日方程法和牛顿-欧拉方程法。拉格朗日方程法通过动势能差异来建立动力学方程，而牛顿-欧拉方程法则利用构件质心的平动和转动来构建动力学模型，特别适用于实时控制。 章节接着详细讨论了刚体的加速度。刚体加速度可以通过对线速度和角速度进行微分来获取，这涉及到坐标系的选择和变换。例如，当坐标系{A}与{B}重合时，可以利用速度向量的表示来推导刚体在不同坐标系下的加速度表达式。 动力学方程的建立是关键，其中包括牛顿方程和欧拉方程，它们是描述物体受力和运动状态之间关系的基础。牛顿-欧拉迭代动力学方程用于计算力矩作用下操作臂的动态响应，而封闭形式的动力学方程则简化了这一过程，便于分析和应用。此外，章节还提到了动力学方程的结构，这对于理解和设计操作臂的控制系统至关重要。 在操作臂动力学方程的拉格朗日公式中，动势能和势能的差异与广义力相联系，这种方法对于建立复杂系统如操作臂的动力学模型非常有用。同时，考虑非刚体效应意味着必须考虑操作臂在运动过程中的变形和其他非线性因素。动力学仿真是验证和优化这些模型的有效工具，它允许在实际操作前预测操作臂的行为。 本章内容涵盖了从基本概念到高级技术的全面讲解，为理解和实现工业机器人操作臂的精确控制提供了理论基础。通过学习这些知识，工程师能够更好地设计和控制机器人系统，满足各种任务需求，包括轨迹规划、力控制和实时性能优化。