晶体结构对称性解析：从点阵到空间群

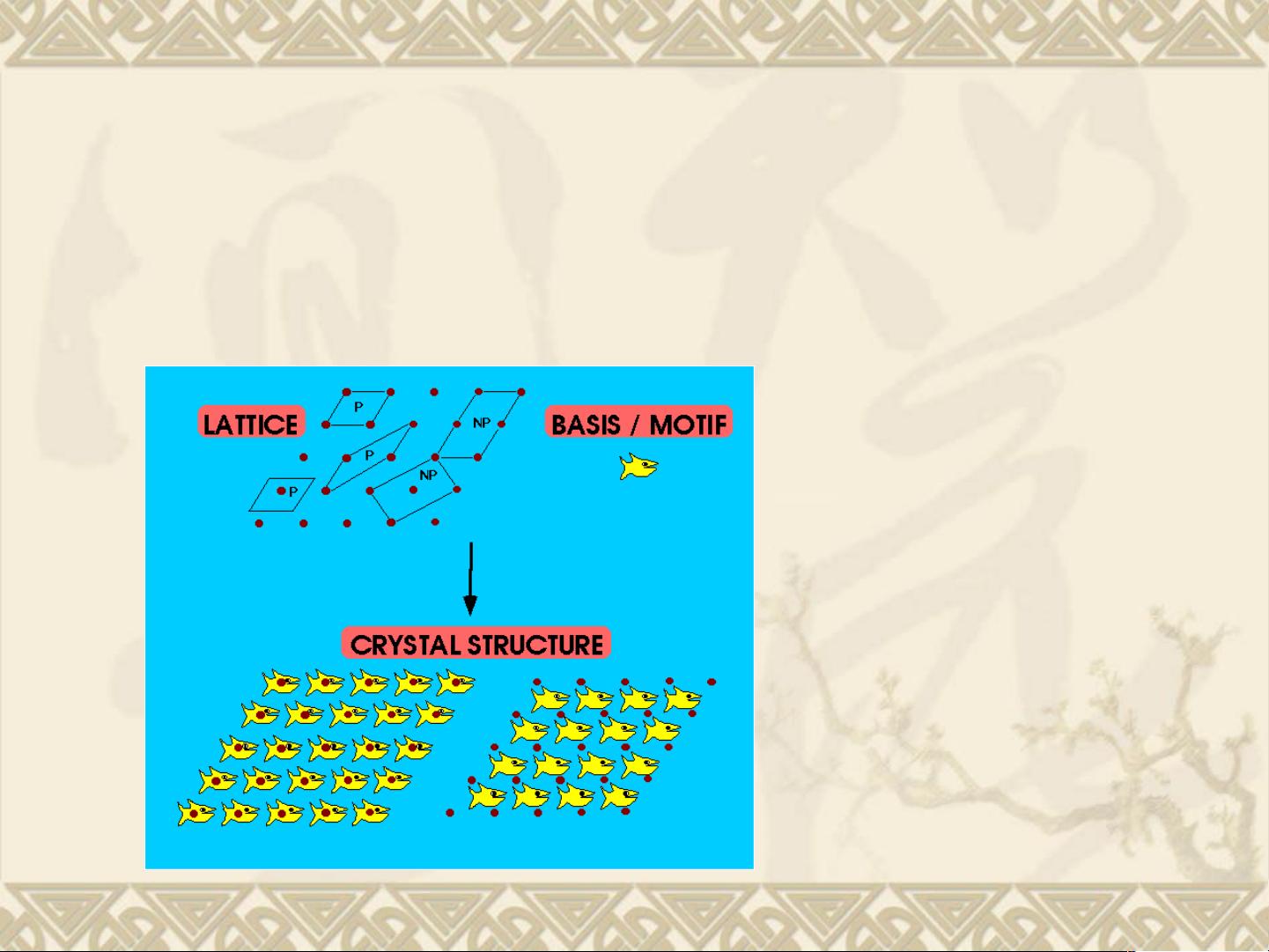
晶体结构的对称性是研究晶体性质的重要方面，它涉及到晶体内部原子排列的规律性和美学。从点阵到空间群的理论是理解这一特性的关键。 首先，晶体的平移对称性体现在三维点阵和晶胞上。点阵是由一系列无限重复的点构成的，这些点在空间中按特定的平移矢量t=ua+vb+wc移动后，能完全复原原有的点阵结构，这里的u、v、w是整数。点阵的这种特性使得晶体在不同方向上具有相同的周期性。晶胞是点阵的一个基本单元，通常是一个平行六面体，其边长a、b、c和夹角关系构成了晶体的几何特征。 晶体学中的对称操作元素包括旋转轴、倒反中心、镜面、反轴、映轴、螺旋轴和滑移面。这些对称元素是晶体对称性的具体表现，它们定义了晶体在特定方向上的不变性。例如，旋转轴是指晶体能绕着某个轴进行多次旋转而不改变其外观，而倒反中心则意味着通过某个点，晶体的上下、前后、左右都能找到与之相对应的结构。 晶体学点群是对晶体对称性的分类，它们根据晶体所能执行的所有对称操作组合来划分。点群分为7种二维点群和32种三维点群，每种点群都有其独特的对称性质。晶系则是根据晶体的对称轴数量和方向来划分的，有七大晶系，如立方晶系、四方晶系、三方晶系等。点阵型式则根据晶胞的形状和大小来定义，如简单立方、体心立方、面心立方等。 空间群是晶体对称性的完整描述，它结合了平移对称和平面群的对称操作。空间群不仅包含了点群的所有对称元素，还考虑了平移对称性，因此可以全面反映晶体的结构特性。空间群符号用于标识特定的空间群，等效点系指的是在空间群中具有相同对称性质的点集合，分数坐标用于描述原子在晶胞内的位置，而不对称单位则是分析晶体结构时选择的最小对称单元。 晶体的对称性不仅影响其外观，更决定了其物理和化学性质。例如，各向异性是指晶体在不同方向上的物理性质差异，自范性则表明晶体倾向于自发形成规则的多面体形状。对称性对晶体的光学、电学、热学等性能有着深远影响。 从点阵到空间群的理论深入探讨了晶体结构的对称性，这是理解和设计新材料、解释实验观测结果以及预测晶体性能的基础。通过对晶体对称性的深入研究，科学家能够更好地理解和利用自然界的这些奇妙现象。