"图象三级小波变换系数结构-EZW编码解码原理详解"

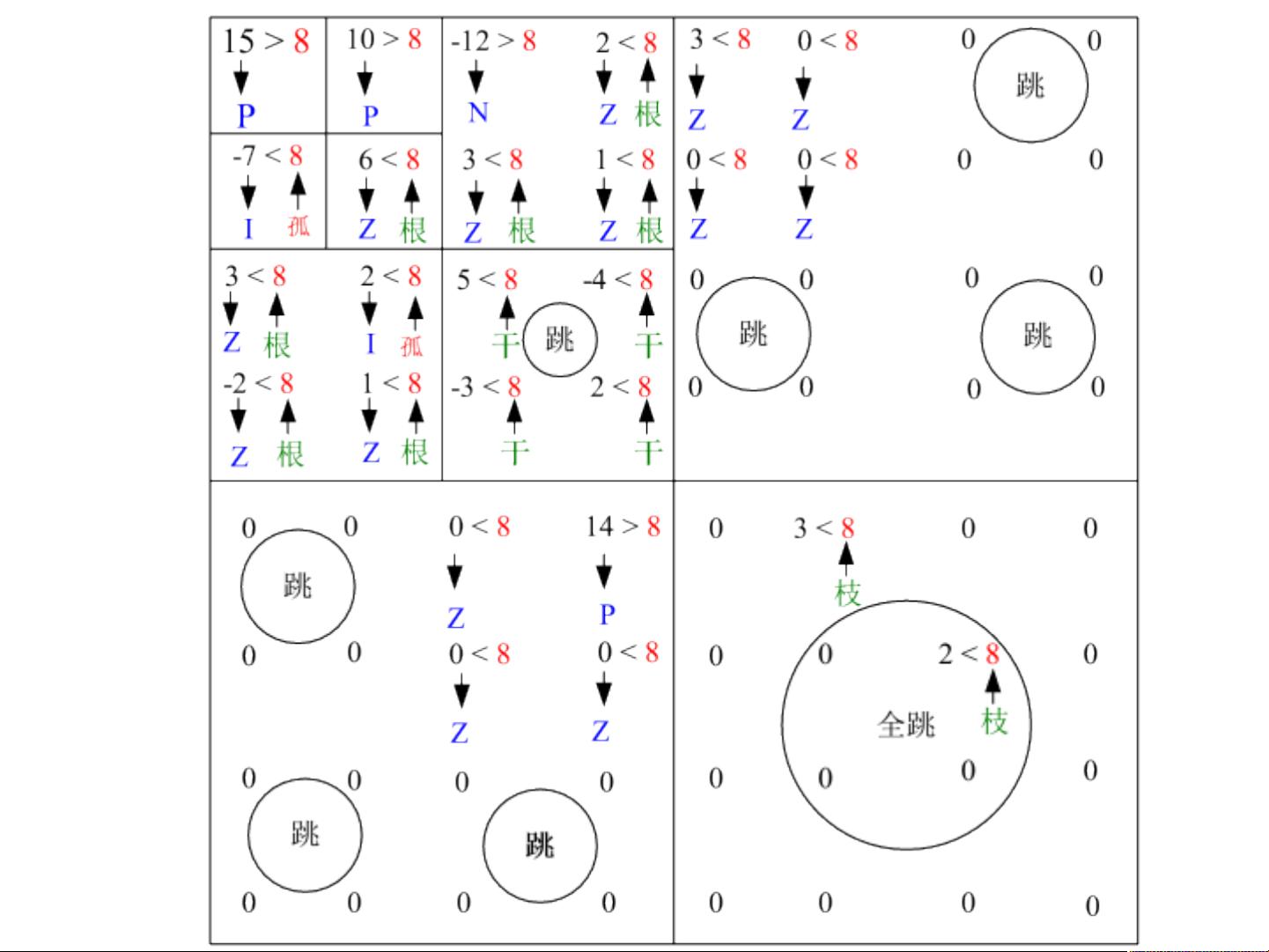
图一是一幅经过三级小波变换后的系数结构，而图二是对应的三级小波变换后的系数结构。图二的系数结构由LL3、HL3、HH3、LH3、HL2、HL1、HH2、LH2和LH1、HH1组成。在EZW编码和解码过程中，我们以一个8×8的原始图像为例。 首先，我们需要了解EZW算法中的一个重要概念：零树。在图一中，可以看到颜色笔所示的路径，这条路径形成了基本的树状结构。由于小波变换要进行隔行隔列抽取，所以前一尺度的4点只能抽成后一尺度的一点，这种1∶4的关系导致了树状结构的形成。 EZW算法的编解码过程如下： 1. 编码过程： - 首先，将系数矩阵中的每个系数按照大小进行排序。 - 在排序后的系数中找到第一个非零系数，并将其加入到编码结果中。 - 对于剩余的系数，根据其相邻的系数情况，分为两种编码方式： - 零树编码（Zero-Tree Coding）：如果一个系数的邻居系数都是零，则将该系数及其所有后代系数都编码为零树，即将零树标记加入到编码结果中。 - 确定性编码（Deterministic Coding）：如果一个系数的邻居系数中有非零系数，则将该系数编码为其绝对值和符号的有限位数表示。 2. 解码过程： - 首先，根据编码结果中的零树标记，重建系数矩阵的结构。 - 按照编码结果中的确定性编码进行解码，恢复各个系数的值。 通过上述编解码过程，我们可以将原始图像通过三级小波变换后的系数矩阵进行高效地压缩和解压缩。EZW算法的优势在于其对系数的稀疏性进行了充分利用，减少了编码和解码的数据量，并且能够在不同精度要求下进行逐步传输和重建。 总之，小波变换的EZW编码和解码是一种常用的图像压缩算法。通过对系数矩阵的编码和解码过程，可以有效地实现图像的压缩和解压缩，从而减少存储空间和传输带宽的占用。此外，EZW编码和解码过程中的零树编码和确定性编码方法能够对系数的稀疏性进行充分利用，提高了压缩算法的效率和质量。