理解和应用聚类算法：从K-means到谱聚类

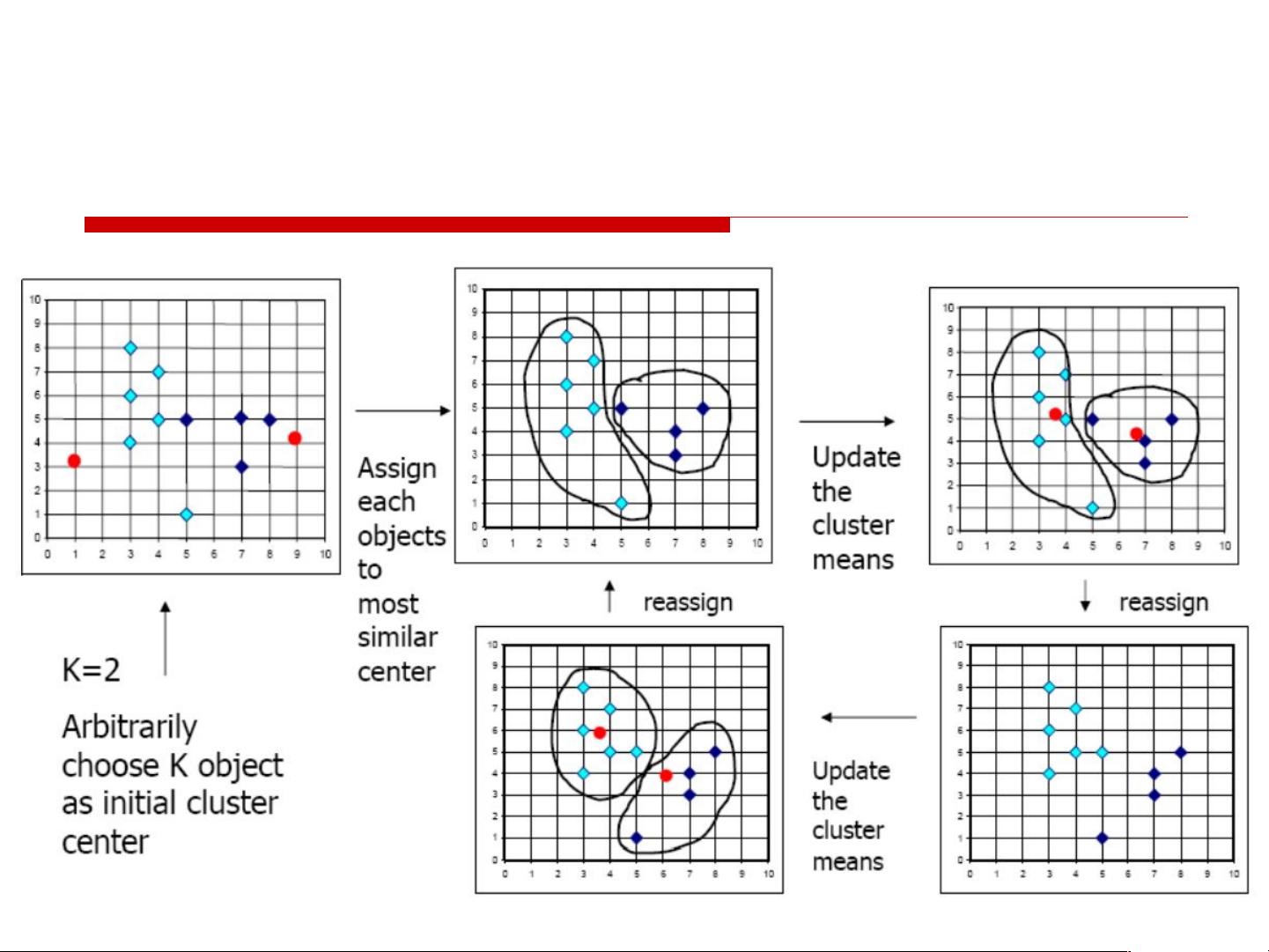
该资源主要介绍了聚类算法的基础知识，包括最大熵模型、决策树、Logistic回归等概念，并重点讲解了K-means聚类、层次聚类、密度聚类（如DBSCAN和密度最大值聚类）以及谱聚类。 在机器学习中，聚类是一种无监督学习方法，用于将数据集中的样本根据其内在相似性分成不同的组或簇，目的是使得同一簇内的样本相似度较高，不同簇间的样本相似度较低。聚类不依赖于预先存在的标签，而是通过数据本身的特性进行分组。 最大熵模型在建立模型时，经常利用熵作为不确定性度量，如在决策树构建过程中，特征选择就可能涉及熵的计算。Logistic回归是一种分类算法，其对数似然函数是凹函数，通过梯度上升法求解得到的参数是全局最优解。 K-means算法是最常用的聚类方法之一，它需要预先设定簇的数量k。算法首先随机选取k个初始中心点，然后将每个样本分配到最近的簇，接着更新簇的中心为该簇所有样本的平均值，这个过程持续进行直至簇中心不再显著变化，即达到收敛。K-means算法对初始中心点的选择敏感，不同的初始化可能导致不同的聚类结果。 层次聚类提供了另一种聚类策略，可以是自顶向下（ divisive）或自底向上（agglomerative）。自底向上方法从每个单独的样本开始，逐步合并相似的样本形成簇。 密度聚类如DBSCAN（Density-Based Spatial Clustering of Applications with Noise）算法，它不依赖于预先设定的簇数量，而是基于样本的密度来识别簇。DBSCAN可以发现任意形状的簇，并且对离群点具有较好的处理能力。密度最大值聚类是另一种基于密度的聚类方法，寻找局部密度最高的点作为簇中心。 谱聚类则是利用数据的相似性矩阵构造图谱，通过图的拉普拉斯矩阵进行特征分解，从而确定簇的数量和簇的结构。这种方法对于非凸形状的簇识别效果较好。 在计算样本之间的相似度时，有多种度量方式，如欧式距离、杰卡德相似系数和余弦相似度。其中，欧式距离是基于欧几里得空间的直线距离，杰卡德相似系数衡量两个集合的交集与并集的比例，余弦相似度则关注两个向量方向的相似性而非大小。 该资源提供了聚类算法的全面概述，涵盖了从基础理论到具体算法实现，对于理解和应用聚类技术具有很高的价值。