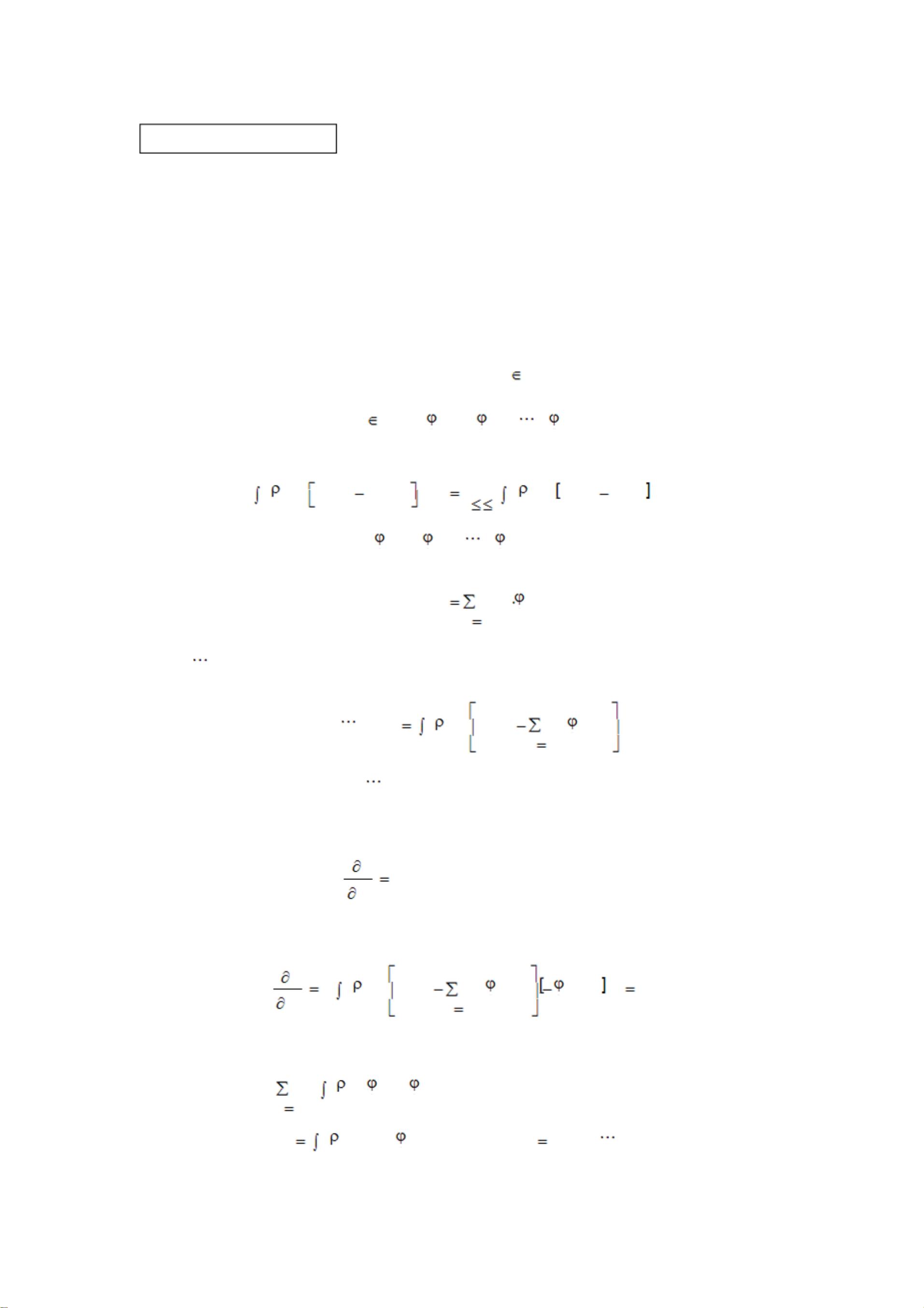MATLAB最佳平方逼近实现及理论分析

"MATLAB最佳平方逼近试验文档" 在数值分析中，最佳平方逼近（Least Squares Approximation）是一种常见的方法，用于寻找一个函数的最佳近似解。在这个试验中，我们探讨了如何使用MATLAB来求解函数$f(x)=e^x$在区间$[-1,1]$上的二次和三次最佳平方逼近多项式。 最佳平方逼近的核心思想是找到一个函数集合中的特定函数，使得该函数与目标函数在指定区间上的平方误差之和最小。对于给定的函数$f(x)$和区间$[a,b]$，最佳平方逼近函数$S_*(x)$是在集合$\text{Span}\{x^0, x^1, \ldots, x^n\}$中的多项式，使得积分$\int_a^b (f(x) - S_*(x))^2 dx$达到最小值。 对于二次逼近，我们需要找到一个二次多项式$S_*(x) = a_0 + a_1x + a_2x^2$，而三次逼近则需找到$S_*(x) = a_0 + a_1x + a_2x^2 + a_3x^3$。求解这些逼近的系数$a_0, a_1, \ldots, a_n$可以通过解决一组线性代数方程来实现。 利用多元函数极值的必要条件，我们可以构建方程组。对于二次逼近，方程组为： \[ \begin{cases} \int_{-1}^{1} f(x)(1)dx = \int_{-1}^{1} S_*(x)(1)dx \\ \int_{-1}^{1} f(x)x dx = \int_{-1}^{1} S_*(x)x dx \\ \int_{-1}^{1} f(x)x^2 dx = \int_{-1}^{1} S_*(x)x^2 dx \end{cases} \] 对于三次逼近，方程组则扩展为： \[ \begin{cases} \int_{-1}^{1} f(x)(1)dx = \int_{-1}^{1} S_*(x)(1)dx \\ \int_{-1}^{1} f(x)x dx = \int_{-1}^{1} S_*(x)x dx \\ \int_{-1}^{1} f(x)x^2 dx = \int_{-1}^{1} S_*(x)x^2 dx \\ \int_{-1}^{1} f(x)x^3 dx = \int_{-1}^{1} S_*(x)x^3 dx \end{cases} \] 这里的$f(x)$是原函数，$S_*(x)$是我们要找的最佳逼近多项式。通过函数内积的定义，我们可以将这些积分表示为： \[ \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & -1 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \end{bmatrix} = \begin{bmatrix} \int_{-1}^{1} f(x)dx \\ \int_{-1}^{1} x f(x)dx \\ \int_{-1}^{1} x^2 f(x)dx \\ \int_{-1}^{1} x^3 f(x)dx \end{bmatrix} \] 解这个线性方程组，我们可以得到最佳平方逼近多项式的系数。在MATLAB中，可以使用`linalg.solve`或`inv`函数来求解这个线性系统，从而得到近似多项式。 这个试验展示了如何运用MATLAB进行数值计算，解决最佳平方逼近问题。MATLAB的强大在于其内置的数学函数库和优化工具，使得这类复杂的数学问题变得易于处理。通过实践，我们可以更深入地理解最佳平方逼近的概念，并掌握在实际问题中应用的方法。