W. Long, T. Wu and X. Liang et al. / Expert Systems With Applications 123 (2019) 108–126 111
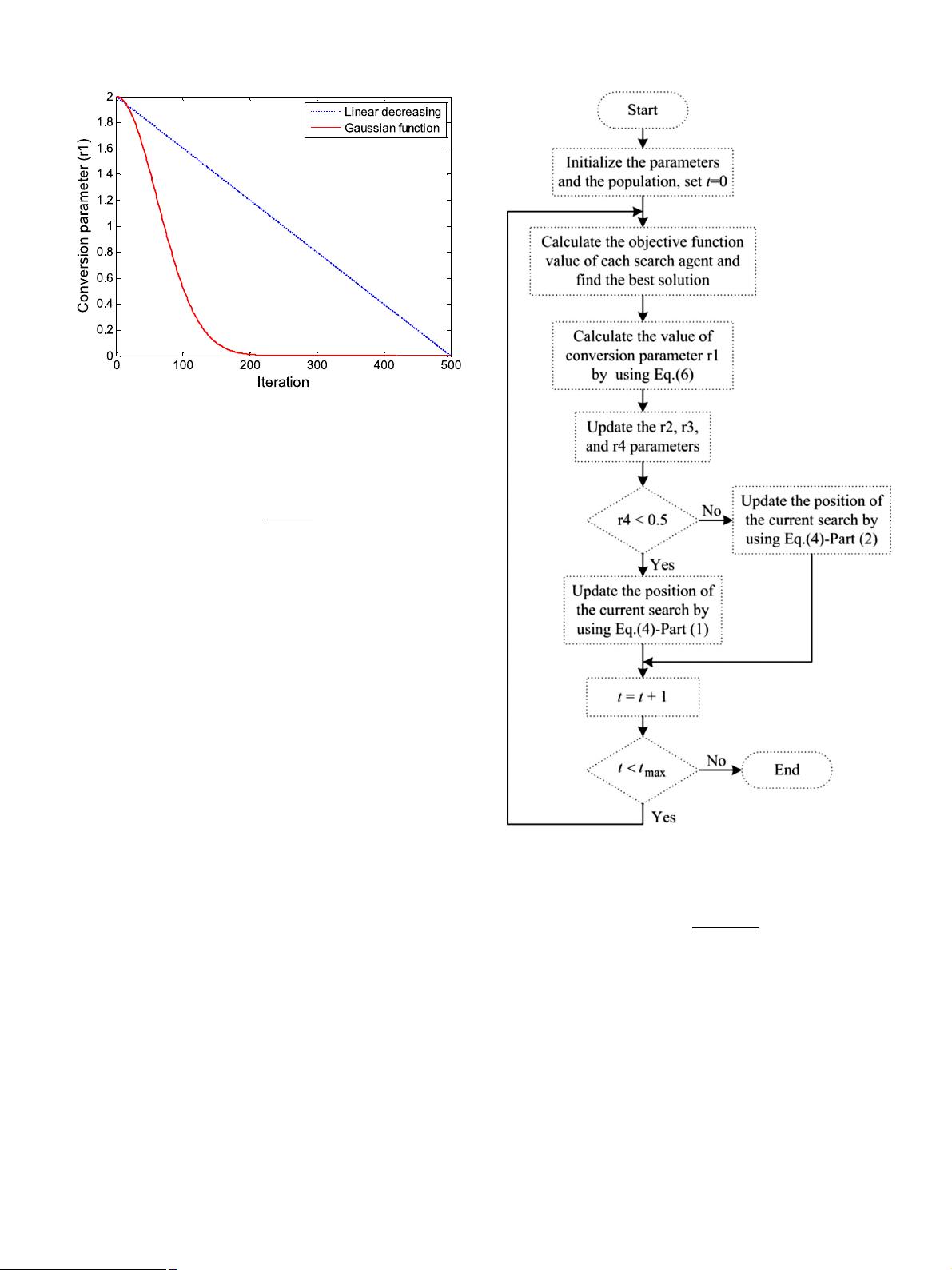
Fig. 1. The conversion parameter r
1
curve of linear decreasing and Gaussian func-
tion.
decreased from a start value ( w
start
) to an end value ( w
end
) accord-
ing to the following equation:
w
(
t
)
= w
end
+
(
w
start
− w
end
)
×
t
max
−t
t
(5)
Compared with the position-updating Eq. (2) in the conven-
tional SCA, Eq. (4) can yield more information to the position-
updating equation and generate a more promising candidate so-
lution to improve the performance of the proposed SCA algorithm.
4.2. Modified conversion parameter strategy
All population-based optimization algorithms aim to achieve
a balance in both the exploration and exploitation to obtain the
promising regions of the search space and eventually converge to
the global optimum. In the population- based optimization ap-
proaches, exploration refers to the ability to investigate various un-
known regions in the search space to identify the global optimum.
Exploitation refers to the ability to apply the knowledge of the pre-
vious satisfactory solution to obtain better solutions ( Luo, Wang, &
Xiao, 2013 ). Further, the abilities of exploration and exploitation in
every population-based search algorithm are applied with specific
operators.
According to Mirjalili (2016) , four primary parameters exist in
the conversional SCA: r
1
, r
2
, r
3
, and r
4
, where r
1
is the most critical
parameter that converts from exploration to exploitation using an
adaptive range in the sine and cosine functions. A larger conversion
parameter r
1
facilitates global exploration, while a smaller conver-
sion parameter ( r
1
) facilitates local exploitation. A suitable selec-
tion of conversion parameter r
1
can provide a balance between
global exploration and local exploitation. However, in the conven-
tional SCA, the value of r
1
decreases linearly from a to zero us-
ing the Eq. (2) . In the beginning stage of the optimization process,
the conversion parameter r
1
for the linearly decreasing strategy is
good at exploration but poor at convergence; in the later stage of
the search process, this strategy is good at exploitation but easily
trapped in the local optima. Additionally, because the search pro-
cess of the SCA is nonlinear and highly complicated, the linearly
decreasing conversion parameter r
1
cannot truly reflect the actual
search process.
Therefore, we herein modify the conversion parameter r
1
equa-
tion described by Eq. (3) , and present a new conversion parameter
r
1
for the nonlinearly decreasing strategy based on the Gaussian
Fig. 2. The flowchart of the proposed ISCA.
function as follows:
r
1
(
t
)
=
(
a
start
− a
end
)
× exp
−
t
2
(
k ×t
max
)
2
+ a
end
(6)
where t indicates the current iteration, t
max
indicates the total
number of iterations, k is the nonlinear modulation index, and
a
start
and a
end
are the initial and final values of constant a , respec-
tively. Fig. 1 shows the comparison curve of the linearly decreasing
strategy and the Gaussian function decreasing strategy.
In summary, we combined the proposed modified position-
updating equation and the modified conversion parameter strat-
egy and developed the ISCA algorithm. The flowchart of the ISCA
is shown in Fig. 2 .
4.3. Computational complexity
The time complexities of the SCA and ISCA are described as fol-
lows: 1) SCA and ISCA initialization require the O ( N ) time, where
剩余18页未读，继续阅读
weixin_38517728
- 粉丝: 5
- 资源: 919
我的内容管理
展开
最新资源
- 贵州煤矿矿井水分类与处理策略：悬浮物、酸性与非酸性
- 醛固酮增多症肾上腺静脉采样对比：ACTH后LR-CAV的最优评估
- 开源云连接传感器监控平台：农业土壤湿度远程监测
- 母婴用品企业年度生产计划线性规划优化模型：实证与应用
- 井下智能变电站：Rogowski线圈电流检测系统的研发与性能验证
- 霍州矿区煤巷稳定性分析及支护策略
- ARM嵌入式系统远程软件更新方案：基于TFTP协议
- 煤炭选煤中汞分布规律与洗选脱汞效果
- 提升码垛机器人性能：拉格朗日动力学模型与滑模模糊控制的应用
- 增强现实技术提升学前手写教学：设计与开发案例
- 不规则工作面沉陷三角剖分算法提升与应用
- 卡尔曼滤波在瞬变电磁干扰压制中的应用研究
- 煤矿安全能力研究：理论与系统构建
- LonWorks总线技术在斜巷运输车辆定位与跑车防护中的应用
- 神东煤炭集团高效煤粉锅炉系统：节能环保新实践
- Ti/SnO2+Sb2Ox/PbO2电极分形维数与电催化性能研究
资源上传下载、课程学习等过程中有任何疑问或建议，欢迎提出宝贵意见哦~我们会及时处理！
点击此处反馈
