拉格朗日乘数法在约束优化问题中的应用

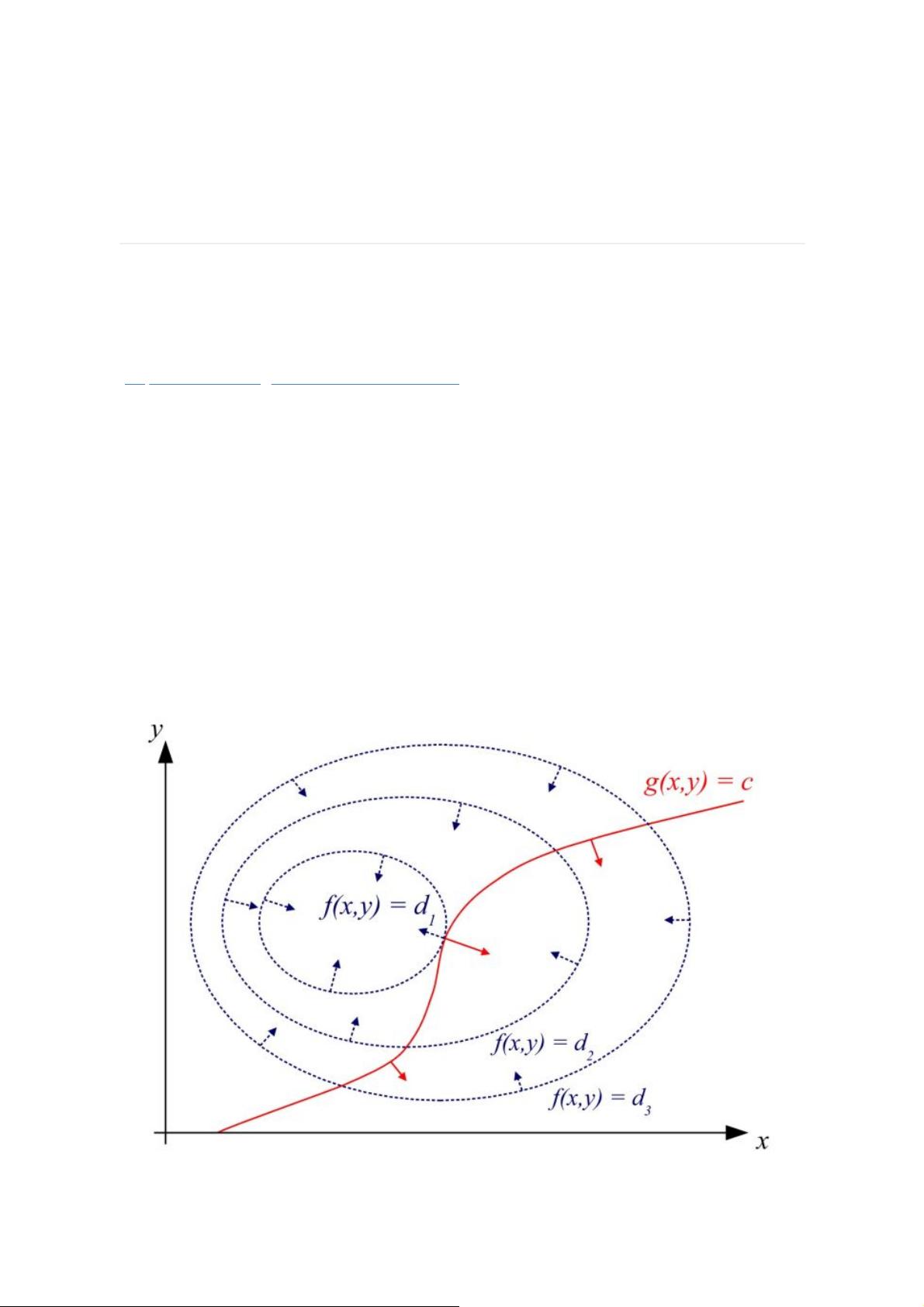
"3.1.0 拉格朗日算法基础-张满满1" 拉格朗日乘数法是解决约束优化问题的一种有效工具，尤其在机器学习和优化理论中广泛应用。它通过引入拉格朗日乘子将一个包含多个变量和约束条件的优化问题转换为一个无约束的优化问题，从而使求解变得更为简洁。 首先，我们要理解拉格朗日乘数法的基本思想。假设我们有一个包含两个变量x和y的函数f(x, y)，并有一个约束条件g(x, y) = c。我们要找到在满足约束g的情况下，使f达到极大或极小值的点。在几何上，我们可以将f的等高线图和g的曲线画出来，当g的曲线与f的等高线相切时，就找到了极值点。 两曲线相切意味着它们在切点处的梯度平行，即∇f(x, y) 和 ∇g(x, y) 成正比。利用这个关系，我们可以构造拉格朗日函数L(x, y, λ) = f(x, y) - λg(x, y)，其中λ是拉格朗日乘子。通过对L求偏导数并设为0，我们可以得到一个包含所有变量和λ的方程组，解这个方程组就可以找到可能的极值点。 拉格朗日乘数法分为两种情况： 1. **等式条件下的求最优解**：对于等式约束，如g(x, y) = c，我们可以构建Lagrangian并求解。这样，原本的等式约束条件被转化为寻找L的极值，从而得到原问题的可行解。然而，这通常只是局部最优解，除非f是凸函数，否则不能保证是全局最优。 2. **不等式条件下的求最优解**：处理不等式约束，如g(x, y) ≤ c，通常需要用到KKT（Karush-Kuhn-Tucker）条件，除了梯度平行外，还需要考虑约束边界的情况。 拉格朗日乘数法的关键在于理解等高线和约束曲线之间的关系： - **相离**：如果等高线和约束曲线没有交点，则不存在满足条件的解。 - **相交**：等高线和约束曲线相交，可能存在多个解，但这些交点并不一定是极值点，因为可能存在其他的等高线使得目标函数的值更大或更小。 - **相切**：当等高线和约束曲线相切时，只有一个交点，且这个点是极值点。此时，两者的梯度平行，即∇f(x, y) = λ∇g(x, y)。 通过这个方程，我们可以找到满足约束条件的点，并进一步判断这些点是否为极值点。在实际应用中，拉格朗日乘数法常用于机器学习中的优化问题，如支持向量机（SVM）的求解，以及在统计建模和工程优化中的各种问题。