回归分析：多项式拟合与误差函数探索

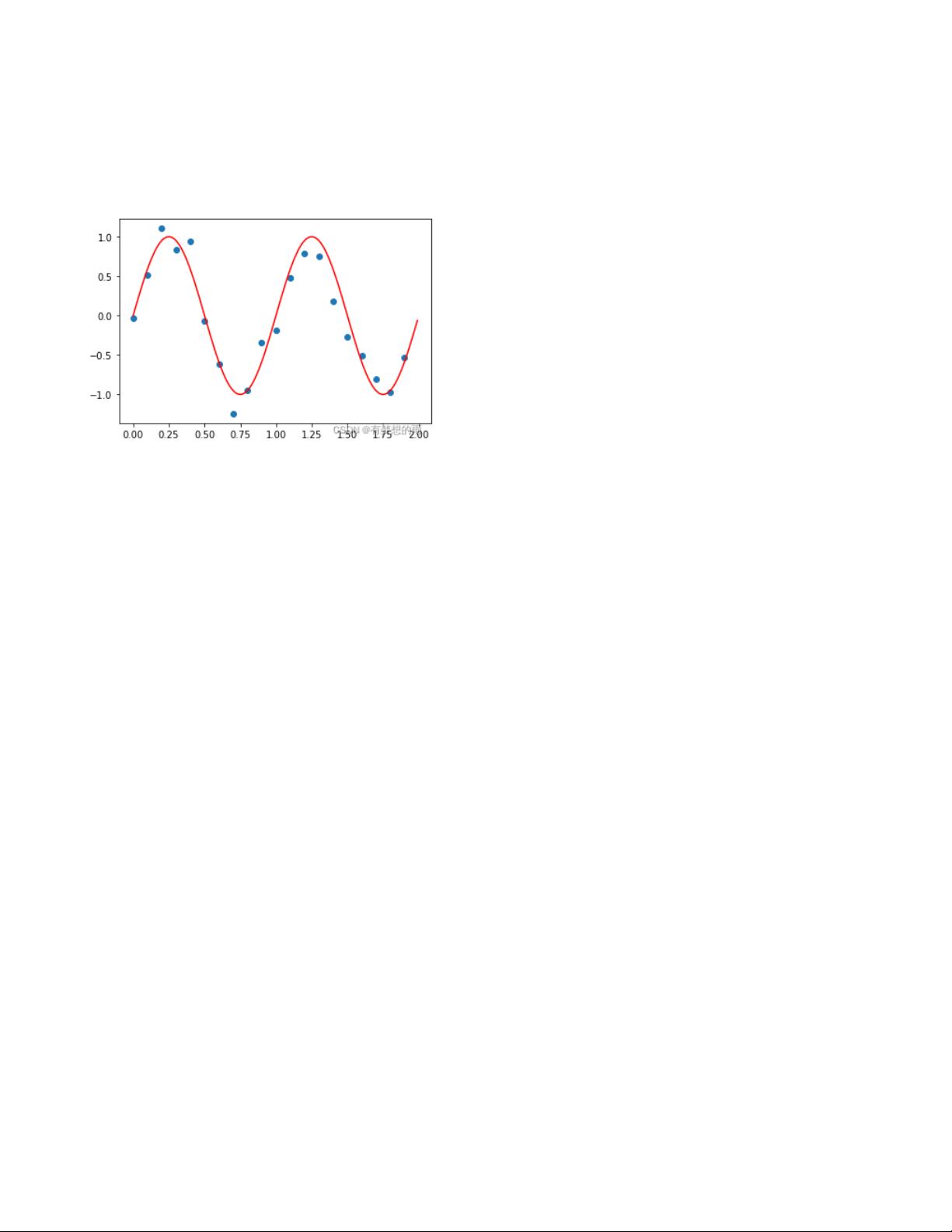
"回归概述-多项式拟合.pdf" 是一份关于回归分析中多项式拟合的文档，主要内容涉及如何利用多项式模型进行数据拟合和预测，以及如何处理过拟合和欠拟合的问题。 回归是一种统计学方法，旨在通过已知的输入变量（自变量）预测输出变量（因变量）。在多项式拟合中，我们尝试找到一个最佳的多项式函数，该函数能够尽可能地逼近给定训练数据集中的点。这通常用于发现数据背后的结构，并用于对未来的新数据进行预测。 数据生成过程假设有一个输入变量 \( x \)，输出变量 \( y \) 受到一个潜在函数 \( f(x) \) 和随机噪声的影响。训练集包含 \( N \) 对观测值 \( (x_n, t_n) \)，其中 \( t_n = f(x_n) + \epsilon_n \)，\( \epsilon_n \) 是服从特定分布（例如正态分布）的噪声项。 多项式拟合是回归的一种形式，它使用多项式函数 \( y(x, w) = w_0 + w_1x + w_2x^2 + \dots + w_Mx^M \) 来近似数据点。这里的 \( w_j \) 是待确定的系数，\( M \) 是多项式的阶数。为了找到最佳的系数向量 \( w \)，我们可以最小化误差函数 \( E(w) \)，它是预测值 \( y(x, w) \) 与实际观测值 \( t \) 差的平方和。 误差函数 \( E(w) \) 表示为： \[ E(w) = \frac{1}{2} \sum_{n=1}^{N} (y(x_n, w) - t_n)^2 \] 当误差函数为零时，意味着多项式完美地拟合了所有训练数据点。然而，选择合适的 \( M \) 是关键，因为过低的阶数可能导致欠拟合，过高则可能导致过拟合。欠拟合是指模型过于简单，无法捕捉数据的复杂性，而过拟合则是模型过于复杂，对训练数据过度适应，导致在新数据上表现不佳。 在实践中，我们可以用均方根误差（RMS）来评估不同阶数 \( M \) 的拟合效果。RMS 是误差平方和的平均值的平方根，它提供了对模型预测精度的直观度量。例如，如果 \( M=0 \)（常数项）或 \( M=1 \)（一次多项式）时，RMS 可能较高，表明模型未能有效捕捉数据趋势。相反，当 \( M \) 过大时，RMS 在训练数据上可能很低，但在未见过的数据上会显著增加，表明过拟合现象。 因此，选择合适的 \( M \) 是一个平衡过程，通常需要在模型复杂性和泛化能力之间找到最佳折衷。这可以通过交叉验证、正则化技术或模型选择准则（如 Akaike 信息准则或 Bayesian 信息准则）来实现。在实际应用中，我们不仅追求拟合训练数据，更要确保模型在未知数据上的表现。