中南大学数电习题与解答：逻辑函数化简

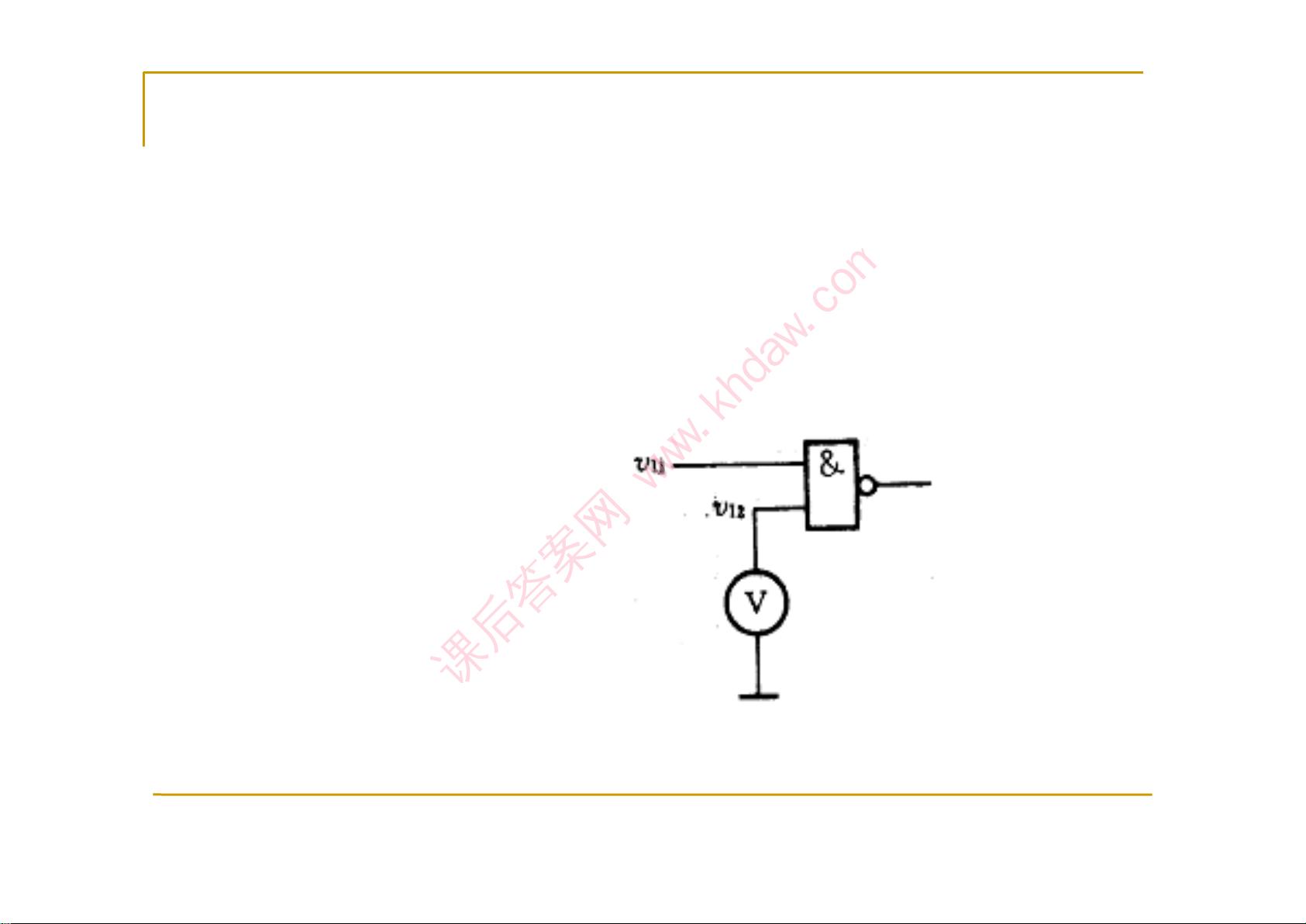
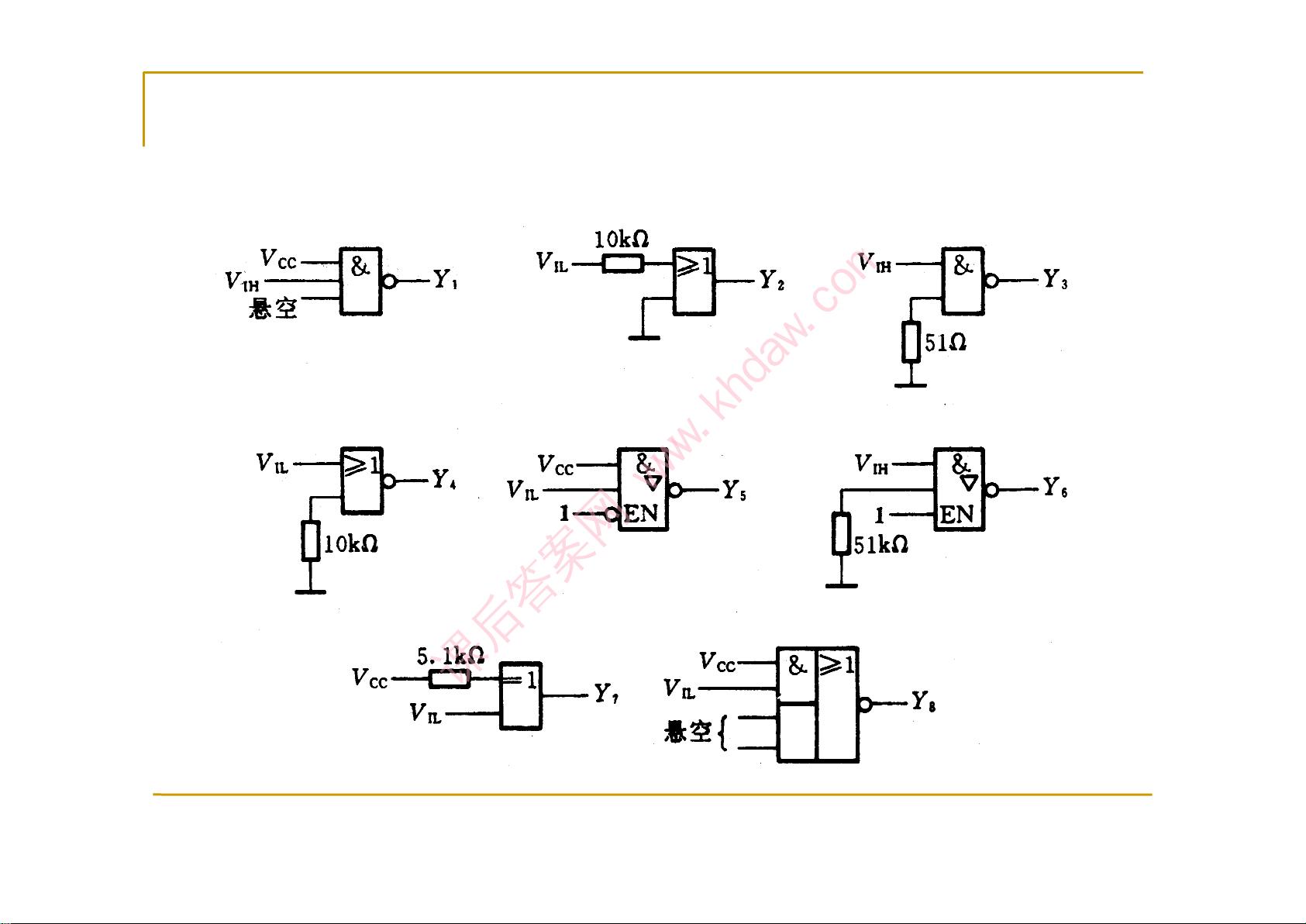
"中南大学数电习题册答案" 这篇资料是关于中南大学电子数字电路（数电）课程的习题解答，适用于中南大学的学生进行学习和复习。资料内容涵盖了解决数电问题的各种练习，包括逻辑函数的简化、逻辑图的解析以及逻辑电路的设计。 1. 逻辑函数化简 习题中提到了将逻辑函数化为最简与或形式，这是数字逻辑中的基础操作。最简与或形式是指通过逻辑代数的基本公式和常用公式，如德摩根定律、分配律、结合律等，将复杂的逻辑表达式简化成最少项之与或的形式，以便于分析和设计电路。例如，给定的逻辑函数(1)Y = AB + B'AB'，可以化简为Y = A'B' + AB，这个过程有助于减少实际电路中的门数量，提高效率。 2. 逻辑图的逻辑函数式及化简 题目要求写出逻辑图的逻辑函数并化简为最简与或式。这是将电路图形转换为数学表达的过程，便于理解电路功能和进行电路设计。例如，一个包含AND、OR和NOT门的电路图，可以通过观察门的输入和输出关系推导出其逻辑函数，然后进行化简。 3. 逻辑电路设计 部分习题要求用与非门和反相器实现特定的逻辑函数。这是在实际电路设计中常见的任务，与非门和反相器是基本的逻辑门单元，通过组合它们可以构建出任何复杂的逻辑函数。例如，实现Y = (A'B')(A'B)C，需要正确连接与非门和反相器，确保最终输出满足给定的逻辑关系。 4. 卡诺图化简法 卡诺图是解决最大项或最小项合并的一种图形工具，常用于化简布尔表达式。通过将变量的取值映射到二维格子上，可以直观地找出能够合并的相邻项。例如，对于Y = AB' + A'C + BC'，对应的卡诺图可以帮助我们找到可以消去的相邻1格，最终得到最简形式。 5. 逻辑函数的约束条件 在某些情况下，逻辑函数会有约束条件，如AB + CD = 0。这意味着A和B不能同时为1，或者C和D不能同时为0。在设计电路时，这种约束可以帮助减少错误和简化设计。 这份习题集涵盖了数字逻辑中的核心概念，包括逻辑函数的化简、逻辑图的理解、逻辑门的使用以及卡诺图的应用，这些都是学习数字电子学不可或缺的部分。通过这些习题的练习，学生可以深入理解和掌握数字逻辑的基本原理和方法。