二维静电场有限差分法求解：不同介质问题分析

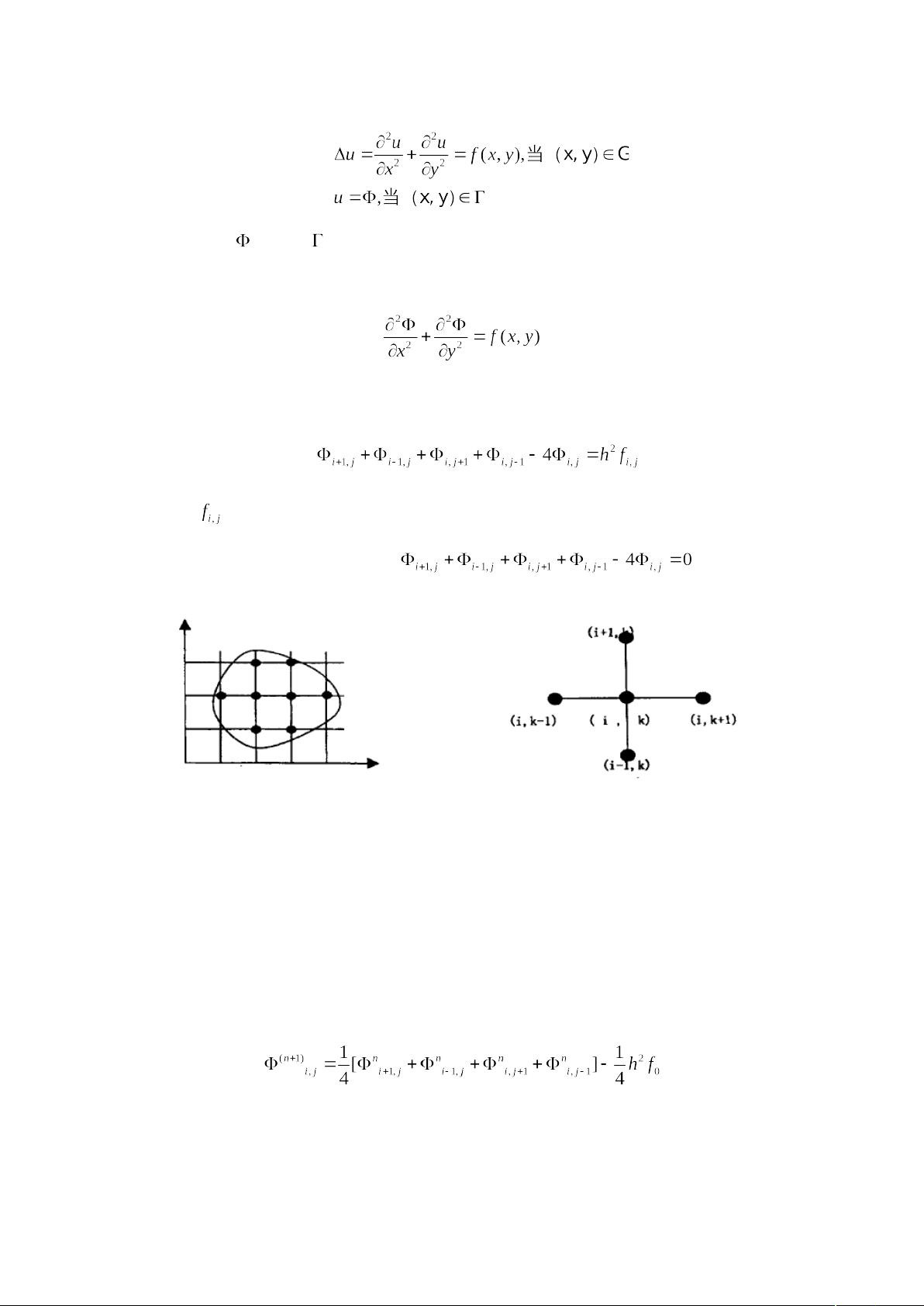
"这篇实验报告详细介绍了如何使用有限差分法求解二维静电场问题，特别是在不同介质分界面下的应用。报告涵盖了从有限差分法的基本概念到具体问题的分析和解决方案，包括MATLAB仿真的结果。" 在计算电磁学中，有限差分法是一种常用的技术，用于数值求解偏微分方程，特别是在处理复杂边界条件和非均匀介质的场景下。此方法的基础是将连续空间离散化为一个网格，通过近似微分运算为差分运算来解决问题。当差分步长趋近于0时，有限差分可以逼近连续微分。 问题1涉及的是单一介质中的二维静电场。在这种情况下，金属槽的横截面被假设为一个二维问题，电位函数受到拉普拉斯方程的约束，这是一个无源且无旋的静电场方程。通过建立适当的差分方程，并在边界上施加零电位（侧壁和底面）和10V电位（顶面）的边界条件，可以求解电位分布、电场强度以及绘制等位线。数值计算的误差和迭代次数也是评估求解质量的重要指标。 问题2则引入了两种不同介电常数的介质，导致了更复杂的边值问题。左侧介质的介电常数不同于右侧，且两者在1/4位置以绝缘隔开。因此，除了拉普拉斯方程外，还需要考虑介质交界处的边界条件。这一变化使得求解更为复杂，需要额外的差分处理来正确模拟电位分布和电场强度在不同介质间的过渡。 在有限差分法中，差分是通过取函数在某一点附近的变化量来近似微分的。例如，函数f(x)在x处的差分可以表示为f(x+h) - f(x)，其中h是差分步长。当h足够小，一阶差分可以作为f'(x)的近似。这种方法允许在计算机上进行数值计算，因为它是离散的，而不是连续的，从而能够处理实际问题中的不连续性和复杂性。 这个实验报告通过两个具体问题展示了有限差分法在计算电磁学中的应用，特别是对于二维静电场在不同介质中的求解。MATLAB仿真结果的提供有助于直观地理解电位分布、电场强度和等位线的形状，同时也验证了所采用的数值方法的准确性。