编译原理作业解析：正则表达式与DFA

"该资源包含了编译原理课程的两次作业答案，主要涉及正则表达式、有限自动机（NFA和DFA）以及语言的补运算。内容包括对正则表达式的自然语言描述，以及如何构造DFA来识别特定语言。作业中还提到了子串与子序列的区别，并探讨了在DFA中‘死状态’的概念及其处理方法。" 在编译原理的学习中，正则表达式是一种用于描述字符串集合的强大工具。作业中提到的第一个问题涉及将正则表达式转化为自然语言描述，例如，`b*(ab*ab*)*` 描述的是所有含有偶数个'a'的'a'和'b'的组合，而`c*a(a|c)*b(a|b|c)*|c*b(b|c)*a(a|b|c)*`则表示所有至少包含一个'a'和一个'b'的'a', 'b', 'c'字符串。 作业中提到了子串与子序列的概念，子串是字符串的一个连续部分，而子序列可以不连续，只要原字符串中的字符顺序保持不变即可。例如，对于字符串"abcde"，"ace"是其子序列但不是子串。 在第二个作业中，重点在于通过正则表达式描述不包含特定子串或子序列的语言。如`b*a*`定义了所有不包含连续的"ab"的字符串，`b*(ab?)*`则排除了包含"abb"的字符串，而`b*a*b?a*`则确保不存在子序列"abb"。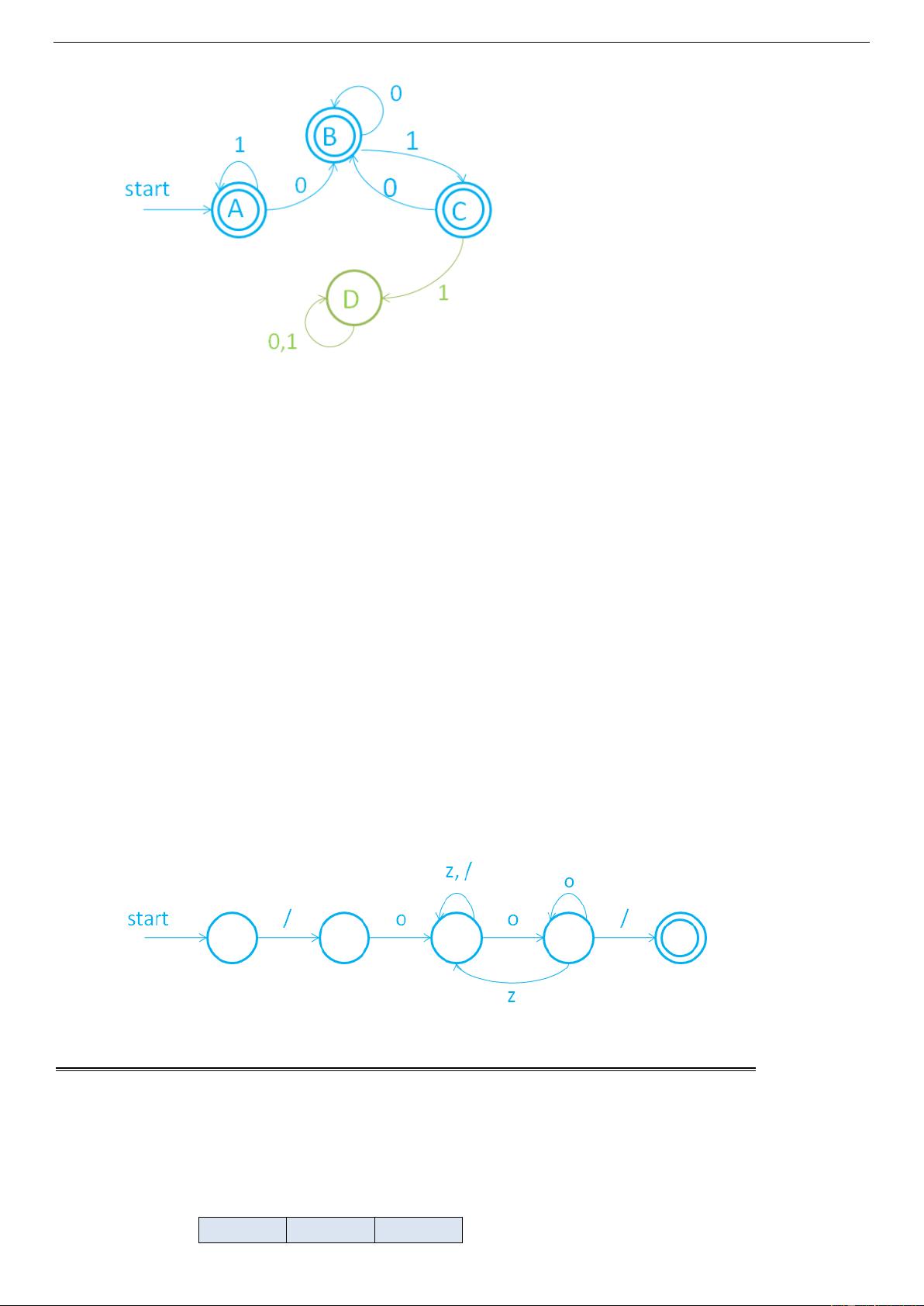 NFA（非确定性有限状态自动机）和DFA（确定性有限状态自动机）是理解正则表达式语言的关键。NFA可以接受一个字符串，即使存在多个路径导致接受状态，而DFA只能有一条路径到接受状态。作业中给出了如何将NFA转换为DFA的方法，同时讨论了在构建DFA时如何处理死状态，即那些无论输入什么符号都无法到达接受状态的状态。 此外，作业还涉及了正则语言的补运算，即找出不被正则表达式描述的所有字符串集合。通过改变接受状态和非接受状态，可以从识别语言L的DFA构造出识别其补集L'的DFA。 这些知识点是编译原理基础的核心，理解和掌握它们对于深入学习编译器设计、形式语言理论以及相关领域至关重要。通过解决此类作业，学生可以提升对正则表达式、有限自动机及其转换的理解，以及如何用它们来描述和识别不同的字符串模式。