图论与网络模型:从哥尼斯堡七桥到现代应用
需积分: 0 79 浏览量
更新于2024-06-30
收藏 479KB PDF 举报
"图与网络模型在多个学科中的应用及重要性"
在数学的世界里,图论是一门研究点与点之间连接关系的学科,它的起源可以追溯到18世纪,瑞士数学家欧拉在其关于"哥尼斯堡的七座桥"的问题中首次引入了这一概念。欧拉通过将陆地抽象为点,桥梁作为连接点的线,构建了一个图的模型,从而解决了困扰哥尼斯堡居民的问题,这也标志着图论的诞生。
1847年,克希霍夫在研究电网络问题时,提出了"树"的概念,为电路理论奠定了基础。随后,凯莱在化学中利用图论分析烷烃的同分异构体,哈密尔顿则提出了"周游世界"游戏,即寻找图中的生成圈,这都是图论在不同领域的早期应用。
随着计算机技术的发展,图论的应用范围迅速扩大,它成为了运筹学中的关键分支,广泛应用于物理、化学、通信、建筑、运筹、生物遗传、心理学、经济学和社会学等多个学科。图论提供了一种强大的工具,能够对具有二元关系的离散系统进行建模和分析,例如,通过图的模型可以解决最短路径问题、最大流问题、最小费用流问题以及匹配问题等网络优化问题。
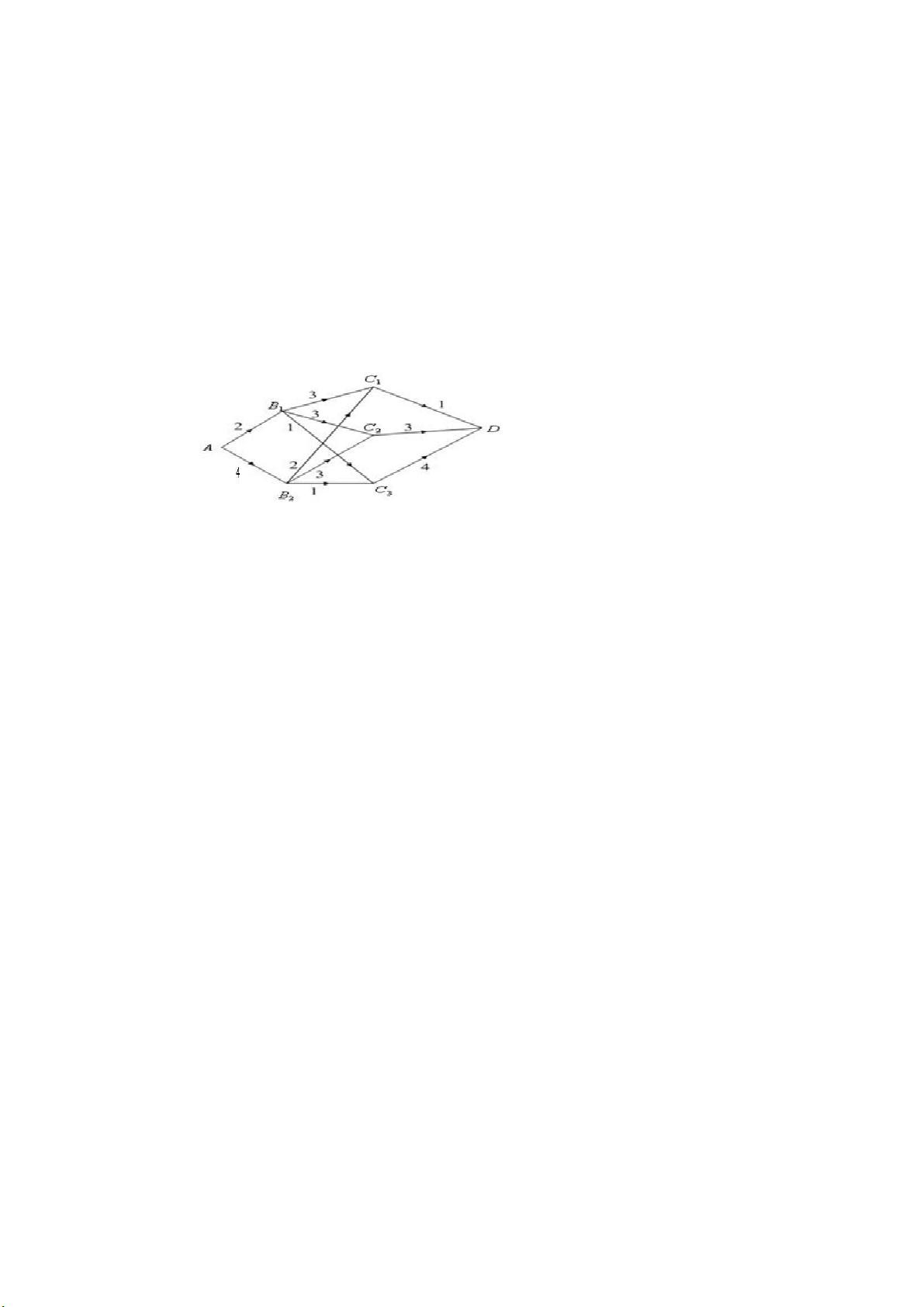
以最短路问题为例,这在物流、交通规划和计算机网络中非常常见。假设一名货车司机需要在最短时间内将货物从起点运输到终点,通过构建一个包含各个节点(如城市、道路)和边(代表道路距离)的图,可以运用Dijkstra算法或Floyd-Warshall算法等图论方法找出最短路径。这些问题的解决对于提高效率、节省资源至关重要。
网络优化问题的另一个典型例子是最大流问题,它在通信网络和物流配送中有着广泛应用。如何在给定的网络中,从源点到汇点最大限度地传递流量,这需要利用Ford-Fulkerson算法或Edmonds-Karp算法等,确保网络资源的充分利用。
最小费用流问题则结合了流量和成本,目标是在满足流量需求的同时,尽可能降低整体费用,这在供应链管理和资源调度中非常实用。最后,匹配问题关注的是在满足一定条件下的最佳配对,如在分配任务或资源分配中找到最优解。
图与网络模型及方法是现代科技中不可或缺的工具,它们不仅解决了许多实际问题,还在不断推动新理论和技术的发展。随着大数据和人工智能的崛起,图论在处理复杂系统和网络分析中的作用只会变得越来越重要。
2022-08-03 上传
2019-05-14 上传
2021-10-15 上传
223 浏览量
175 浏览量
650 浏览量
2025-01-09 上传
788 浏览量
2025-01-03 上传
八位数花园
- 粉丝: 865
- 资源: 281
最新资源
- Lista_de_Exercicios:Lista deExercíciode Algoritmos do Gustavo Guanabara教授
- rust-cas:通过构建与Bazel兼容的内容可寻址商店来测试Rust
- 网络刀客 v3.0
- TW-Shiraz:Shiraz是Tiddlywiki 5的一个小型插件,包含宏,样式表,模板,片段,图像,静态表,动态表,并充当入门工具包
- vc_static_button.rar_RFW_VC static Button_VC++ static Button
- 行业文档-设计装置-一种折叠式太阳能座椅广告棚.zip
- pid控制器代码matlab-Ziegler-Nichols-Tuning-Method:使用Ziegler-Nichols闭环方法针对给定传
- CompletableFuture.zip
- 纯css制作文字随时间变动而变色,文字变色效果,背景透明阴影
- up4
- Curriculum_Vitae:职务経歴书
- 粒子群多目标-程序.rar_UY9_pareto_pareto多目标_多目标 粒子群_自适应粒子群
- 行业文档-设计装置-一种折纸机的机头.zip
- englishTeachers:使用Postgresql的简单应用
- SSM实验室预约管理系统.7z
- ESP8266-01GPIO口模拟I2C LCD1602.rar