MATLAB绘图与函数操作指南

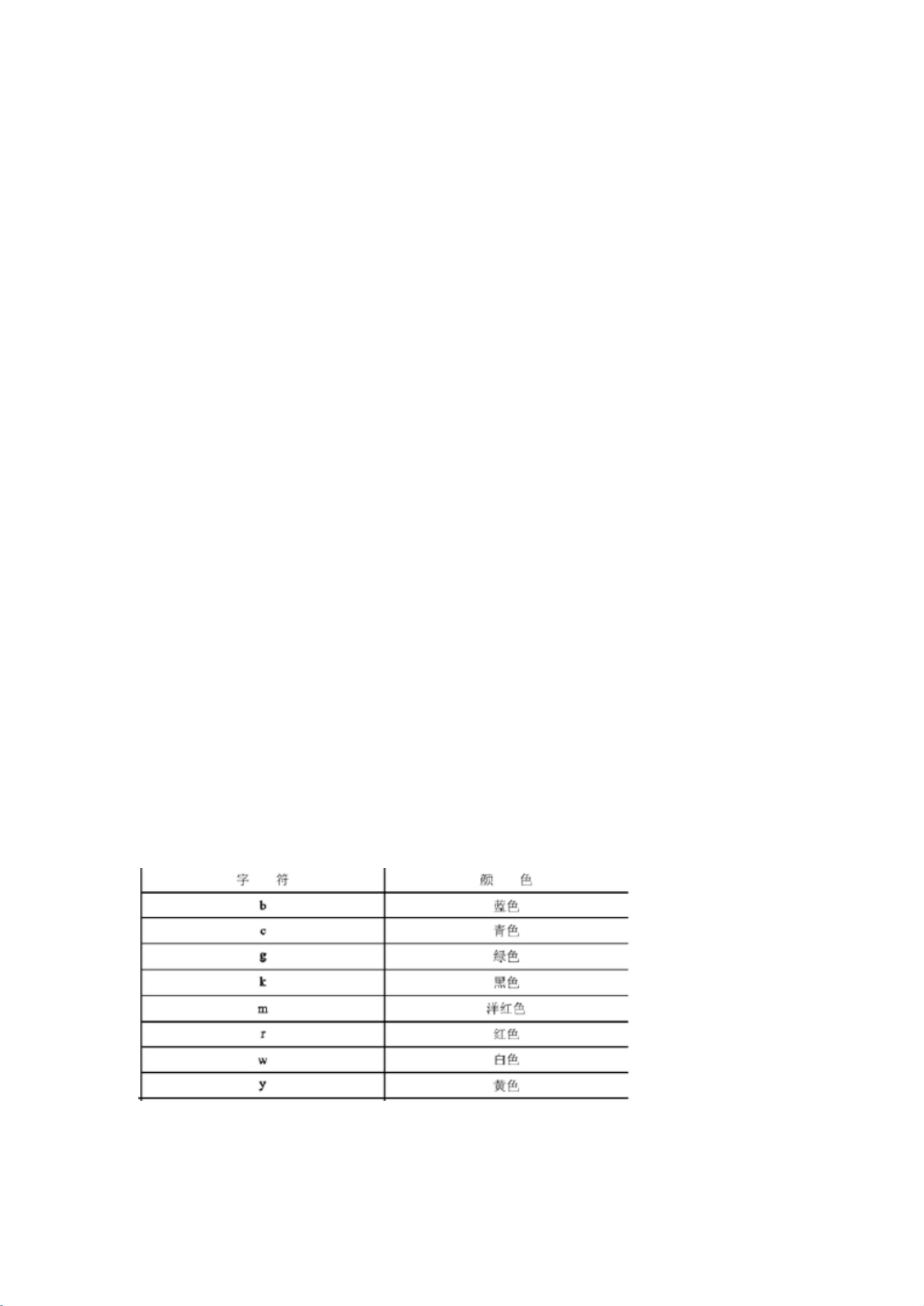
"MATLAB基础操作指南" MATLAB是一款强大的数学计算和数据分析软件，广泛应用于科研、工程和教育领域。以下是一些MATLAB的基础知识点，包括绘图、计算、矩阵操作、函数使用以及数据拟合。 1. 绘图功能： - 标注名称：使用`title('标题')`添加图形的标题，`xlabel('x轴')`和`ylabel('y轴')`用于设置坐标轴的标签。 - 坐标轴上下限：通过`axis([xmin xmax ymin ymax])`设定坐标轴的显示范围。 - 网格线：使用`grid on`开启网格线，调整网格线密度可设置`xtick`的值，如`set(gca,'xtick',[0:2:16])`。 - 绘制函数图形：利用`fplot('表达式',[范围])`绘制函数图形，例如`fplot('sin(1/x)',[0,0.2],'m')`绘制函数并指定颜色（'m'代表红色）。 2. 计算和数据统计： - 平均值：加载数据后，使用`mean(data)`计算平均值。 - 标准差：对于矩阵`C`，使用`std(C)`计算标准差。 3. 矩阵操作： - 矩阵的逆：应用`inv(A)`计算矩阵`A`的逆。 4. 函数应用： - 三角函数：`sin(x)`, `cos(x)`, `tan(x)`分别表示正弦、余弦和正切；它们的反函数如`asin(x)`, `acos(x)`, `atan(x)`对应反正弦、反余弦和反正切。 - 积分计算： - 符号积分：使用`syms`声明变量，然后`int(f(x),x1,x2)`进行积分。 - 数值积分：定义函数`fun`后，使用`quad(fun,a,b)`计算在区间`[a,b]`上的数值积分，例如`I=quad(fun,0,1945)`。 5. 数据拟合： - 多项式拟合：加载`x`和`y`数据后，`polyfit(x,y,n)`进行n次多项式拟合，`p4=polyfit(x,y,4)`表示四次多项式拟合。之后，使用拟合系数构建新的函数并绘制。 - 指定函数拟合：可以自定义函数形式进行拟合，如`y=m(3)*m(1).^x+m(2)`，其中`m(1)`和`m(2)`为待定参数。 示例中的数据`Date`和对应的`x`、`y`值，可以通过`plot`函数结合`hold on`指令绘制原始数据点，并进行拟合线的绘制。 以上就是MATLAB的基本操作介绍，涵盖了从简单的绘图到复杂的数据处理和分析，是进行科学计算和研究的重要工具。