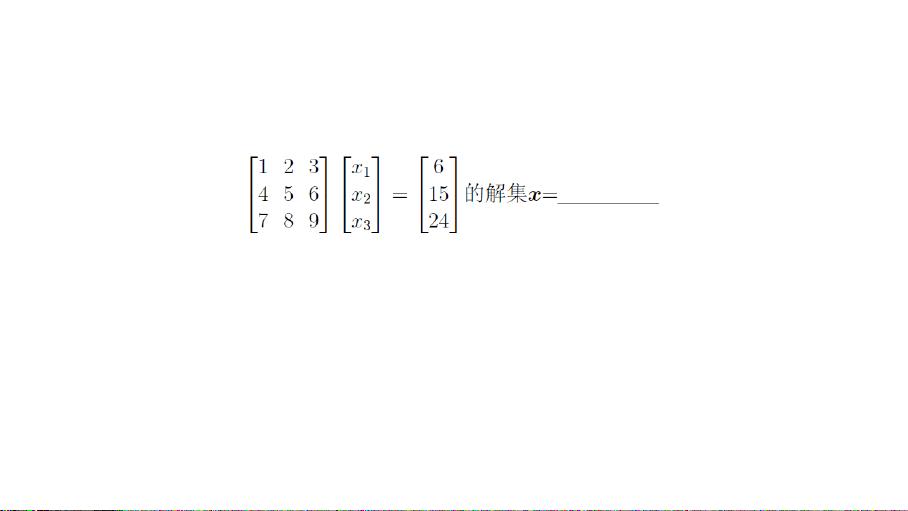"内积、范数与最优解求解的关系"

2.4内积与范数 高级工程数学2021-2022 (1)沈超敏计算机科学与技术学院cmshen@cs.ecnu.edu.cn教书院 上次课的内容回顾了内积和范数的一些公式和性质。在此基础上，我们将进一步推广，并介绍柯西-施瓦茨不等式和勾股定理与欧氏范数的关系。范数在解析连续函数以及优化问题中也起到了重要的作用。通过让范数取最小值，我们可以找到最接近解的点，并得到最优解。 更具体地说，在线性方程组求解最优解时，内积和范数是必不可少的工具。通过运用这些性质，我们可以得出最优解。这样的过程让我们明白了解决方程组的目标不仅仅是确定是否有解，而更重要的是理解优化的过程并朝着最优解的方向努力。 在数学中，欧氏范数是一个重要的概念，它用来衡量向量的长度。欧氏范数具有以下特性： 1. 正性：∥x∥ > 0，并且当且仅当向量x等于零向量时，欧氏范数为零。 2. 齐次性：对于任意实数r，有∥rx∥ = |r| · ∥x∥。 3. 三角不等式：对于任意向量x和y，有∥x+y∥ ≤ ∥x∥ + ∥y∥。 柯西-施瓦茨不等式是一个非常有用的数学定理，它表明对于任意两个向量x和y，内积的绝对值不会超过它们的范数之积。具体而言，柯西-施瓦茨不等式可以表示为： |⟨x,y⟩| ≤ ∥x∥ · ∥y∥， 其中⟨x,y⟩表示向量x和y的内积。 勾股定理是另一个与内积和范数相关的重要定理。在欧几里得空间中，勾股定理指出，在直角三角形中，直角边的平方之和等于斜边的平方。在这种情况下，欧氏范数即为求解勾股定理的平方根。 范数不仅仅适用于向量，还可以用来描述连续函数。通过最小化函数之间的范数差异，我们可以找到最接近的函数，并得到最优解。 总而言之，内积和范数是高级工程数学中重要的概念和工具。它们不仅可以用于解决线性方程组和优化问题，而且在连续函数的分析和最优化中也起到了关键作用。通过理解和运用内积和范数的性质，我们可以得出最优解，并在实际问题中取得更好的结果。