Python编程面试精华：问题示例与改进指南

需积分: 25 67 浏览量更新于2024-07-17 收藏 493KB PDF 举报

《编程面试要素：内幕指南》是一份《编程面试元素》(Elements of Programming Interviews, EPI)的示例文件，由Adnan Aziz、Tsung-Hsien Lee和Amit Prakash共同编撰。该书旨在通过实际问题展示其结构、内容、风格和深度，特别关注编程面试中的技术层面，而不涉及非技术性面试技巧。本书提供了丰富的算法问题实例，适合准备求职者和面试官参考。 Adnan Aziz是得克萨斯大学奥斯汀分校电气与计算机工程系的教授，专注于应用算法的研究和教学。他拥有加州大学伯克利分校的博士学位，本科毕业于印度理工学院坎普尔分校。Aziz有着丰富的行业经验，曾在谷歌、高通、IBM等公司工作，并在软件初创企业任职。他的学术背景和实践经验使他在书中提供了深入且实用的编程面试指导。这份样本仅展示了书中问题的部分内容，旨在让读者了解EPI如何组织和呈现面试技巧。它可能包括但不限于数据结构、算法分析、设计模式、系统设计以及对特定编程语言如Python的理解和应用。对于那些希望通过解决实际问题提升自己编程面试技能的人来说，这本书是不可或缺的资源。如果你在阅读过程中发现任何可以改进的地方，或者想分享关于面试趋势的专业见解，作者非常欢迎读者提供反馈。你可以在Amazon.com上购买完整版的《编程面试元素》，获取更多详细内容和全面指导。同时，Aziz教授的个人经历和研究背景也为读者提供了宝贵的行业洞见，特别是在Python编程面试场景中。《编程面试要素：内幕指南》是一本旨在帮助求职者提升面试表现、了解行业动态，并通过实战练习提升算法和编程能力的实用工具。无论是面试者还是教育工作者，都能从中获益匪浅。

Chapter

Binary Trees

The method of solution involves the development of a theory of ﬁnite

automata operating on inﬁnite trees.

— “Decidability of Second Order Theories and Automata on Trees,”

M. O. Rabin, 1969

A binary tree is a data structure that is useful for representing hierarchy. Formally,

a binary tree is either empty, or a root node r together with a left binary tree and a

right binary tree. The subtrees themselves are binary trees. The left binary tree is

sometimes referred to as the left subtree of the root, and the right binary tree is referred

to as the right subtree of the root.

Figure 6.1 gives a graphical representation of a binary tree. Node A is the root.

Nodes B and I are the left and right children of A.

314

271

257

401

641

561

271

E K

height = 5

depth 0

depth 1

depth 2

depth 3

depth 4

depth 5

Figure 6.1: Example of a binary tree. The node depths range from 0 to 5. Node M has the highest

depth (5) of any node in the tree, implying the height of the tree is 5.

Often the root stores additional data. Its prototype is listed as follows:

1 template < typename T >

2 struct BinaryTreeNode {

3 T data;

4 unique_ptr < BinaryTreeNode <T>> left , right;

5 };

Each node, except the root, is itself the root of a left subtree or a right subtree. If l

is the root of p’s left subtree, we will say l is the left child of p, and p is the parent of l;

10 Binary Trees

the notion of right child is similar. If a node is a left or a right child of p, we say it is a

child of p. Note that with the exception of the root, every node has a unique parent.

Usually, but not universally, the node object deﬁnition includes a parent ﬁeld (which

is null for the root). Observe that for any node there exists a unique sequence of

nodes from the root to that node with each node in the sequence being a child of the

previous node. This sequence is sometimes referred to as the search path from the

root to the node.

The parent-child relationship deﬁnes an ancestor-descendant relationship on

nodes in a binary tree. Speciﬁcally, a node is an ancestor of d if it lies on the search

path from the root to d. If a node is an ancestor of d, we say d is a descendant of that

node. Our convention is that x is an ancestor and descendant of itself. A node that

has no descendants except for itself is called a leaf.

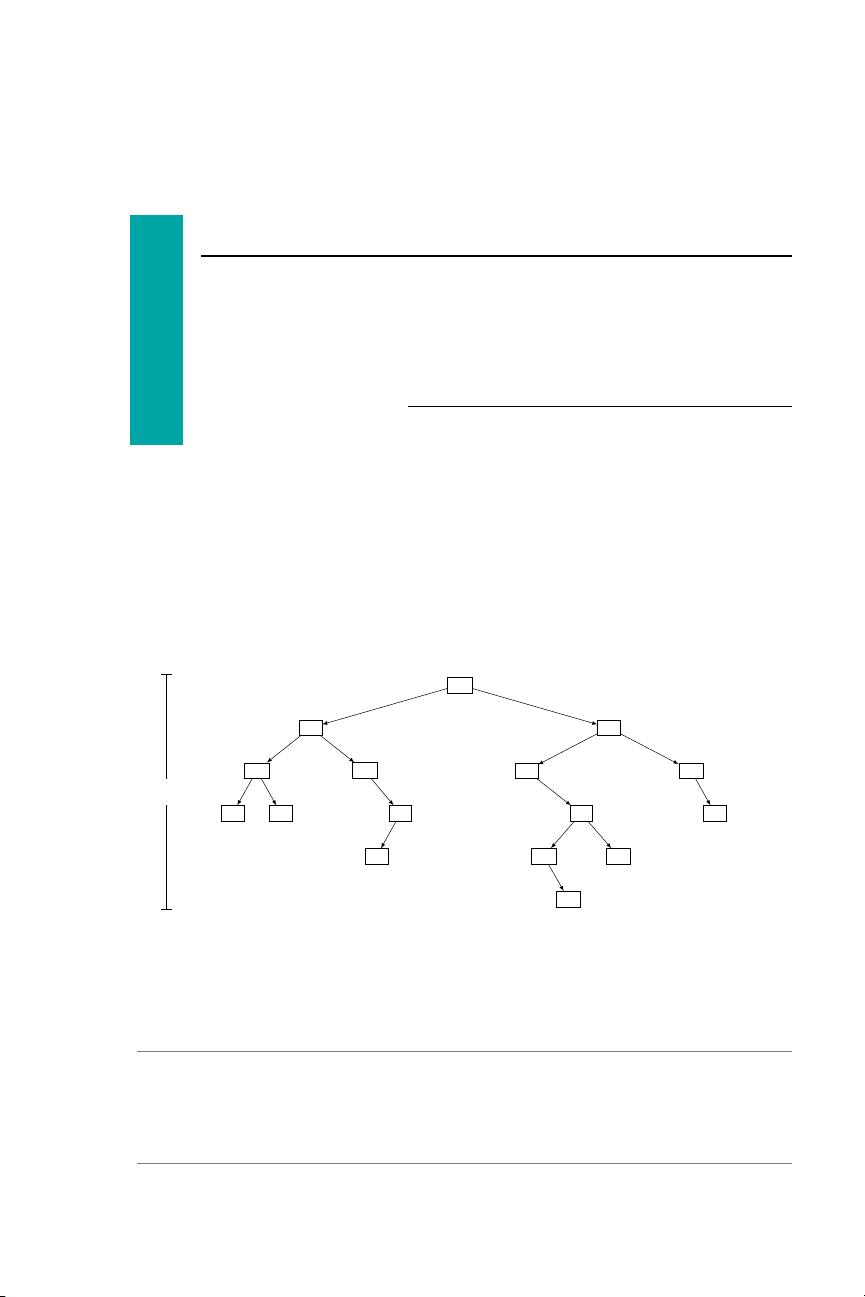
The depth of a node n is the number of nodes on the search path from the root to

n, not including n itself. The height of a binary tree is the maximum depth of any

node in that tree. A level of a tree is all nodes at the same depth. See Figure 6.1 on

the previous page for an example of the depth and height concepts.

As concrete examples of these concepts, consider the binary tree in Figure 6.1 on

the preceding page. Node I is the parent of J and O. Node G is a descendant of B. The

search path to L is hA, I, J, K, Li. The depth of N is 4. Node M is the node of maximum

depth, and hence the height of the tree is 5. The height of the subtree rooted at B is 3.

The height of the subtree rooted at H is 0. Nodes D, E, H, M, N, and P are the leaves

of the tree.

A full binary tree is a binary tree in which every node other than the leaves has two

children. A perfect binary tree is a full binary tree in which all leaves are at the same

depth, and in which every parent has two children. A complete binary tree is a binary

tree in which every level, except possibly the last, is completely ﬁlled, and all nodes

are as far left as possible. (This terminology is not universal, e.g., some authors use

complete binary tree where we write perfect binary tree.) It is straightforward to

prove using induction that the number of nonleaf nodes in a full binary tree is one

less than the number of leaves. A perfect binary tree of height h contains exactly

h+1

− 1 nodes, of which 2

are leaves. A complete binary tree on n nodes has height

blg nc.

A key computation on a binary tree is traversing all the nodes in the tree. (Travers-

ing is also sometimes called walking.) Here are some ways in which this visit can be

done.

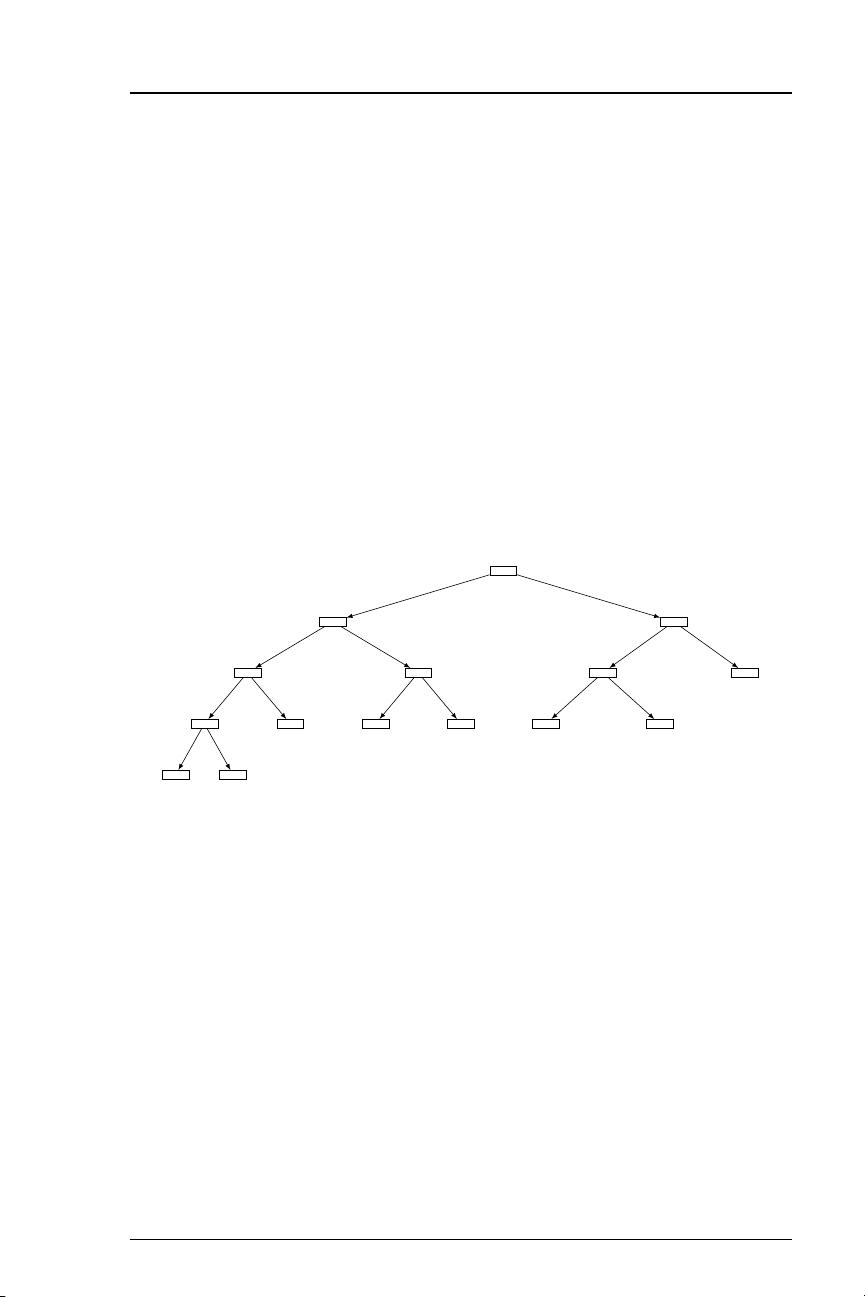
• Traverse the left subtree, visit the root, then traverse the right subtree

(an inorder traversal). An inorder traversal of the binary tree in Fig-

ure 6.1 on the previous page visits the nodes in the following order:

hD, C, E, B, F, H, G, A, J, L, M, K, N, I, O, Pi.

• Visit the root, traverse the left subtree, then traverse the right subtree

(a preorder traversal). A preorder traversal of the binary tree in Fig-

ure 6.1 on the preceding page visits the nodes in the following order:

hA, B, C, D, E, F, G, H, I, J, K, L, M, N, O, Pi.

ElementsOfProgrammingInterviews.com

剩余74页未读，继续阅读

LanceCheng

粉丝: 0

Python编程面试精华：问题示例与改进指南

Elements of Programming interviews

Elements of Programming Interviews：The Insiders高清.pdf版

Elements of programming interviews 高清非扫描 英文原版

python_heroku_sample:python_heroku_sample

machine_learning_mastery_with_python_sample_slightlybcn_machinel

PETA_report_template__Python__monitoring_report1__sample_size_summary:样本量汇总监测报告1

python_sample_shared_module

Learning_ROS_for_Robotics_Programming_Second_Edition_Sample

SAMPLE.rar_驱动编程_Python_

NetSDK_Python_Programming Manual_V1.0.0_NetSdk_test_

最新资源

Elements of programming interviews 高清非扫描英文原版

PETA_report_templatePythonmonitoring_report1__sample_size_summary:样本量汇总监测报告1