"图的广度遍历实例及相关概念"

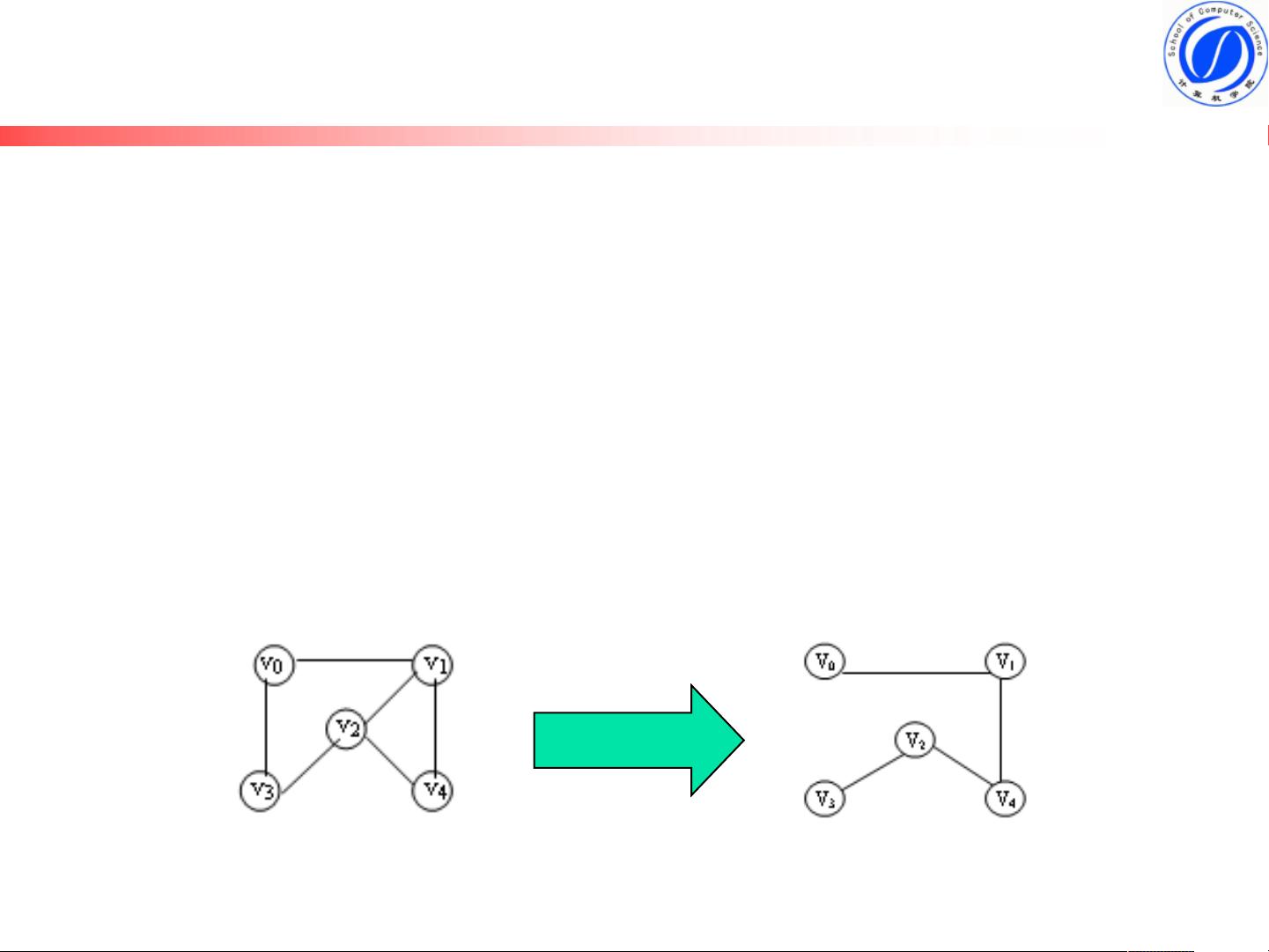
广度遍历实例如下所示： 给定一个图G，根据广度遍历算法，从初始顶点v0开始，依次访问与当前顶点相邻的未访问顶点，直到所有顶点都被访问完毕。广度遍历的访问路径如下：v0 -> v1 -> v2 -> v3 -> v4 -> v5 -> v6 -> v7。 具体的动态过程如下： - 第一步，从初始顶点v6开始遍历，访问v6，标记v6为已访问。 - 第二步，访问v5，标记v5为已访问。 - 第三步，访问v2，标记v2为已访问。 - 第四步，访问v1，标记v1为已访问。 - 第五步，访问v4，标记v4为已访问。 - 第六步，访问v0，标记v0为已访问。 - 第七步，访问v7，标记v7为已访问。 - 第八步，访问v3，标记v3为已访问。 根据以上过程可以得出广度遍历的访问路径为v6 -> v5 -> v2 -> v1 -> v4 -> v0 -> v7 -> v3。 图是一种非常重要且广泛应用的数据结构。在图中，顶点表示一个实体，边表示实体之间的关系。图可以用于描述各种实际问题，如社交网络中的好友关系、地图中的路径搜索等。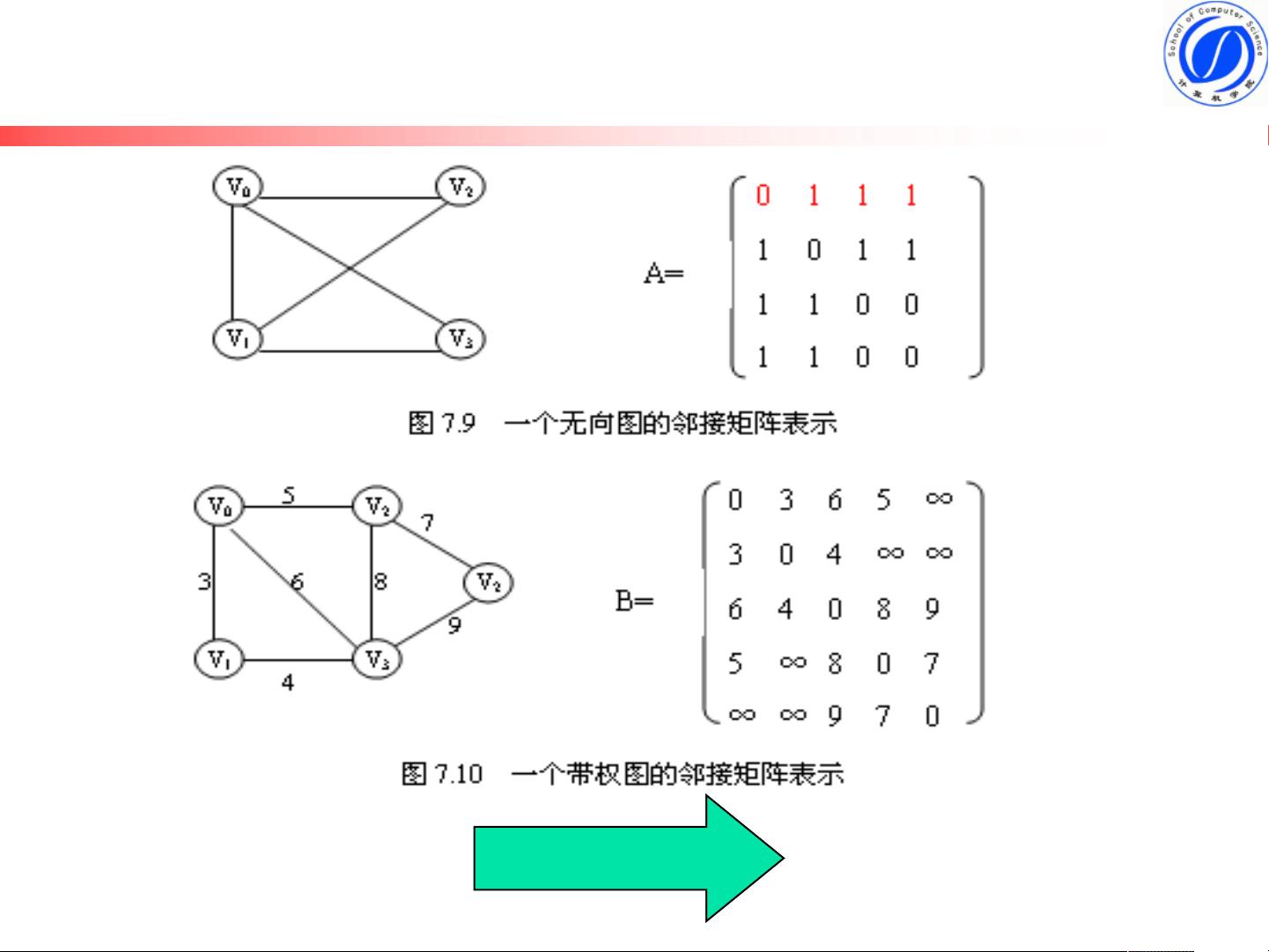 图的存储结构有多种方式，常见的有邻接矩阵和邻接表。邻接矩阵是一个二维数组，其中的元素表示两个顶点之间是否存在边。邻接表则是用链表的方式存储图的每个顶点及其相邻的顶点。 图的遍历操作有两种常见的方法，即广度优先遍历和深度优先遍历。广度优先遍历按层次访问图的顶点，先访问离初始顶点最近的顶点，然后逐层向外扩展。深度优先遍历则是从初始顶点出发，一直沿着一条路径向下访问，直到某个顶点没有未访问的相邻顶点为止，然后回溯到上一个顶点，继续访问其他未访问的相邻顶点。 图的遍历可以应用于解决图的许多典型问题，如最短路径问题、最小生成树问题等。最短路径问题是在一个有权图中找到从一个顶点到另一个顶点的最短路径。最小生成树问题是在一个带权连通图中找到一个权值最小的生成树，使得该生成树包含图中的所有顶点。 总结一下，图是由顶点和边构成的数据结构，可以用于描述各种实际问题。图的遍历操作有广度优先遍历和深度优先遍历，广度优先遍历按层次访问顶点，深度优先遍历以深度优先访问的顺序访问顶点。图的遍历可以应用于解决最短路径问题、最小生成树问题等。掌握图的相关概念和遍历算法对于理解和解决实际问题具有重要意义。