图形几何变换深入解析:从二维到三维
需积分: 18 109 浏览量
更新于2024-07-28
收藏 1.53MB PPT 举报
"本资源详细介绍了图形矩阵在二维和三维图形处理中的应用,包括图形的几何变换、消隐技术、光照处理、裁剪技术和生成方法。适合图形开发初学者学习,内容涵盖CAD/CAM技术基础,如点的表示、变换矩阵、几何变换原理以及二维图形的基本变换等。"
在计算机图形学中,矩阵扮演着至关重要的角色,特别是在二维和三维图形的处理中。图形矩阵是一种数学工具,用于描述图形的几何变换,如平移、旋转、缩放、镜像和错切等。这些变换对于构建和修改图形至关重要。
首先,我们需要理解点的表示。在二维空间中,一个点可以用它的横坐标x和纵坐标y来表示,形成一个位置向量。在矩阵形式下,这个点可以表示为一个2×1的列向量。例如,一个三角形的三个顶点可以通过一个3×2的矩阵来表示。
变换矩阵则是实现图形变换的核心。如果一个点的位置向量与一个变换矩阵相乘,得到的新位置向量就代表了变换后点的新坐标。变换矩阵的特定元素决定了变换的类型和程度,例如,比例因子会影响缩放,旋转角度会影响旋转,而平移向量则控制图形的移动。
在二维图形的几何变换中,常用的变换包括:
1. **缩放**:通过改变变换矩阵的对角元素(a和d)来实现,可以单独或同时在x轴和y轴上放大或缩小图形。
2. **对称/镜像**:通过设置矩阵的非对角元素(b和c)为非零值,可以实现沿特定轴的镜像变换。
3. **旋转**:通过设置适当的旋转角度,矩阵的非对角元素(b和c)可以实现绕任意点的旋转。
4. **错切**:改变非对角元素(b和c)的值,可以对图形进行错切变形。
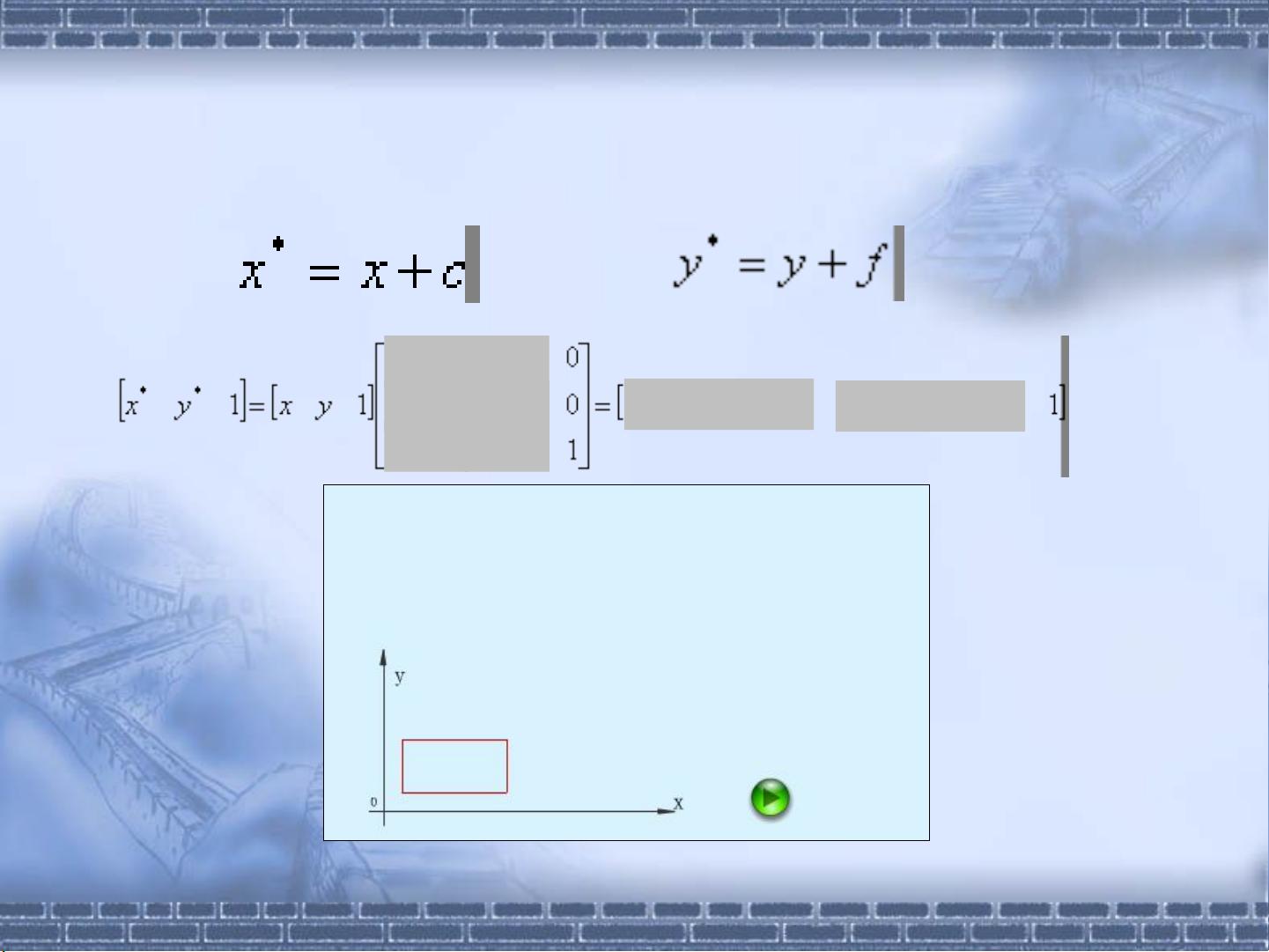
5. **平移**:通过设置矩阵的最后两行(e和f)来实现,改变图形在x轴和y轴上的位置。
对于更复杂的二维和三维图形,变换矩阵通常是3×3的齐次矩阵(二维)或4×4的齐次矩阵(三维)。这种矩阵能够处理图形的多个顶点,通过将整个顶点坐标矩阵与变换矩阵相乘,可以一次性完成所有顶点的变换,从而高效地更新整个图形。
此外,图形的其他处理技术,如消隐、光照处理和裁剪,也是图形矩阵应用的重要领域。消隐技术用于确定图形在视图中哪些部分应该被隐藏,光照处理则模拟真实世界中的光线交互,增强图形的视觉效果。图形裁剪则用于确保超出视口范围的部分不显示。
在实际的CAD/CAM系统中,图形是由其顶点坐标、拓扑关系和表达模型定义的。通过图形的几何变换,可以创建出复杂、动态的图形效果。因此,理解和掌握图形矩阵对于图形开发人员来说是非常基础且必要的技能。
2010-11-23 上传
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
小新提摸
- 粉丝: 1
- 资源: 5
最新资源
- 虚拟人中台相关方案文档
- unity 3D文字系统源码VText.zip
- madgrad:MADGRAD的JAX实现
- SimpleHUD:SimpleHUD是一款易于使用但美观的Android HUD(或对话框)
- 汇编语言程序设计(资料+视频教程).rar
- 信呼协同办公OA系统 v2.1.8
- meelouth.github.io:网站
- bank-java:一个用 Java 编写的带有 GUI 的基本银行程序
- 亚马逊交易-crx插件
- stylex
- Data-Analysis-Project-in-Python:Python中Fifa 18数据集的数据分析。 该项目包括可视化和用于预测目的的机器学习
- glslmath:C ++仅限头文件的库,可模拟GLSL数学-开源
- TongYWPF.Template.NumberOne202303DemoK
- 剁手党买家秀助手-crx插件
- ExpandTabView-master
- React