数字信号处理中的基2时间抽取FFT算法及其结构特点的简介

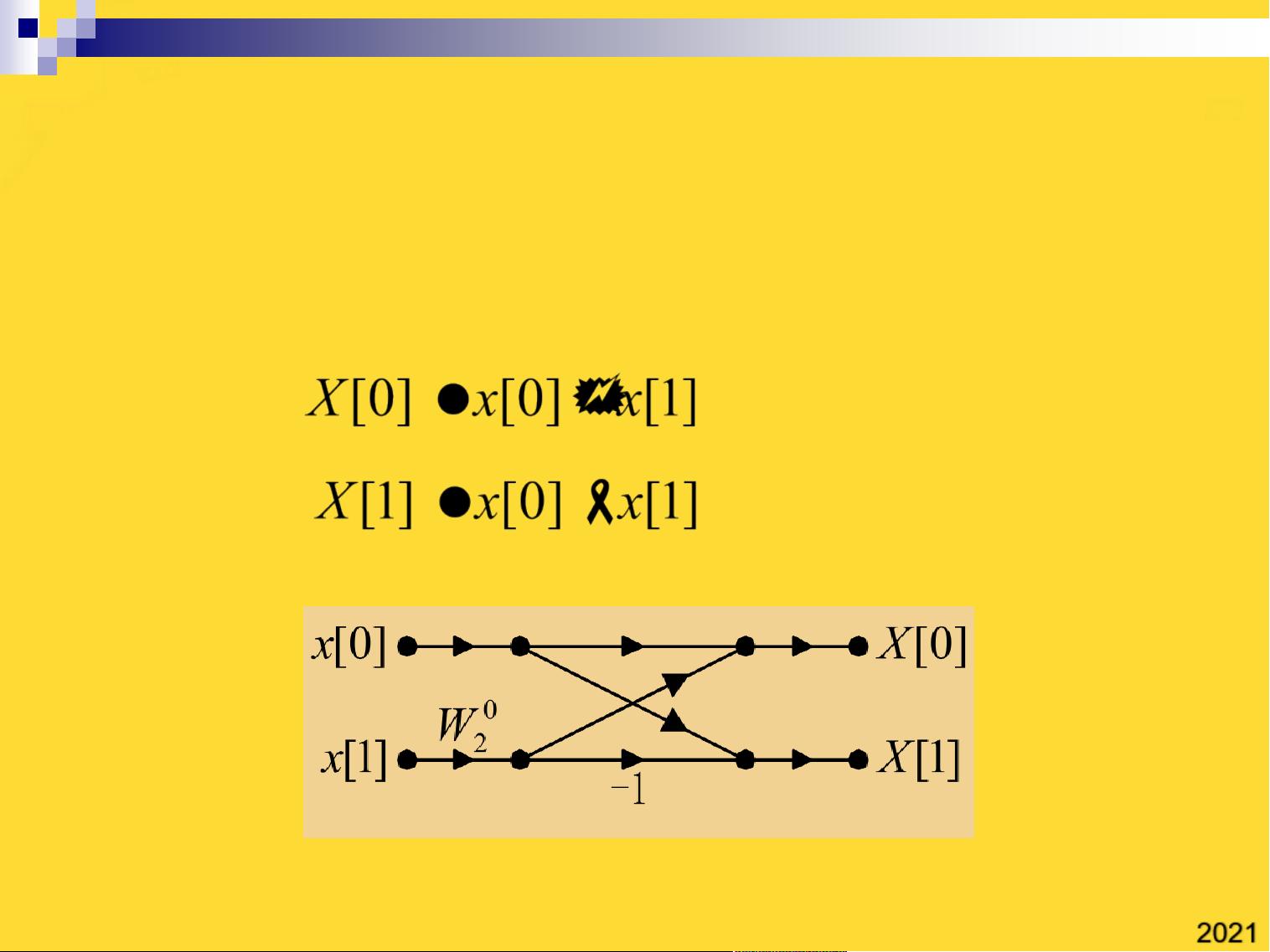
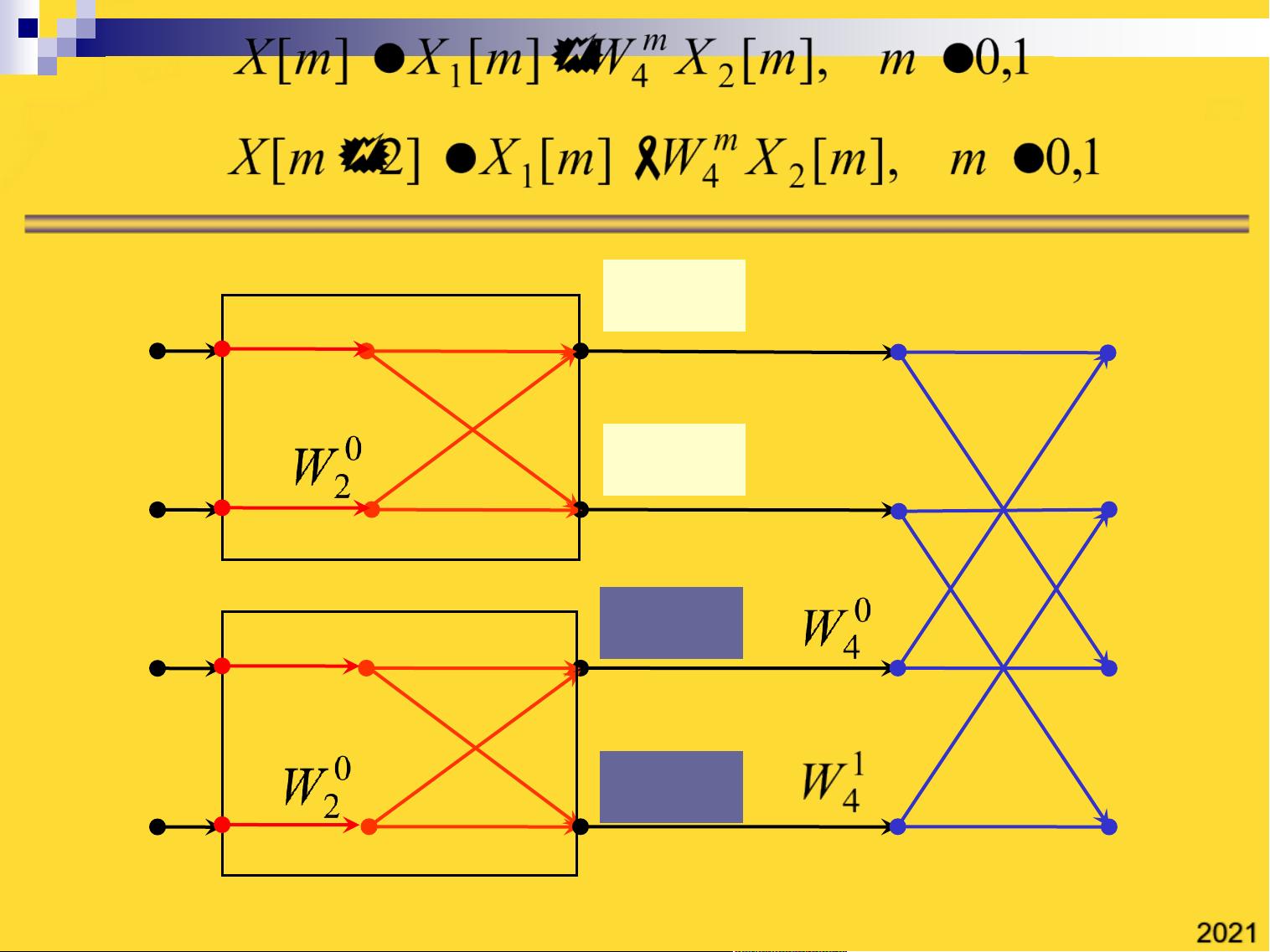
华侨大学自动化专业数字信号处理ppt4(与“抽取”相关共44张).pptx；华侨大学自动化专业数字信号处理ppt4(与“抽取”相关共44张).pptx;第3章 离散傅里叶变换的快速算法（FFT）一、基2时间抽取FFT算法二、基2频率抽取FFT算法三、FFT算法的实际应用四、基4时间抽取FFT算法五、混合基FFT算法问题的提出N点序列DFT的计算复杂度复数加法N(N-1)复数乘法N 2如何提高DFT的运算效率？解决问题的思路1. 将长序列DFT分解为短序列的DFT，再将短序列的DFT合成为长序列的DFT2. 利用旋转因子的周期性、对称性、可约性。旋转因子的性质(1) 周期性(2) 对称性(3) 可约性一、基2时间抽取FFT算法1. 基2时间抽取FFT算法原理2. 基2时间抽取FFT算法流图3. 基2时间抽取FFT算法的计算复杂度4. 基2时间抽取FFT算法结构特点1. 基2时间抽取FFT算法原理（1）分解将长度为N的时域序列x分解为两个长度为N/2的短序列x1、x2偶数点序列奇数点序列这两个短序列的N/2点DFT为（2）合成2. 基2时间抽取FFT算法流图 基2时间抽取蝶形运算的信号流图X1[m]X2[m]X[m]X[m N/2]-12点序列DFT运算流图N=2x[k] 本段描述讲述了华侨大学自动化专业数字信号处理的PPT，其中第三章主要介绍了离散傅里叶变换的快速算法（FFT）。该章节中包含了基2时间抽取FFT算法、基2频率抽取FFT算法、FFT算法的实际应用以及其他相关算法。问题提出了如何提高DFT（离散傅里叶变换）的运算效率，并提出了两种解决思路。第一种思路是将长序列DFT分解为短序列的DFT，再将短序列的DFT合成为长序列的DFT。第二种思路是利用旋转因子的周期性、对称性和可约性。随后，详细介绍了基2时间抽取FFT算法的原理、流图和计算复杂度，并列举了该算法的结构特点。其中，基2时间抽取FFT算法通过将长度为N的时域序列分解为两个长度为N/2的短序列，并对这两个短序列进行N/2点DFT的计算，然后再进行合成，得到长度为N的DFT结果。最后，给出了基2时间抽取FFT算法的蝶形运算的信号流图和12点序列DFT的运算流图。整个描述主要集中在基于基2时间抽取的FFT算法的原理和实现方法，以及如何提高DFT运算效率的问题。