MATLAB数字图像处理:傅立叶变换详解
PPT格式 | 2.52MB |
更新于2024-06-29
| 94 浏览量 | 举报
"matlab《数字图像处理》第8章傅立叶变换完美版资料.ppt"
本资料详细讲解了数字图像处理中的一个重要概念——傅立叶变换,特别是在MATLAB环境下的实现。主要内容包括一维傅立叶变换、二维傅立叶变换、傅立叶变换的性质、MATLAB实现以及傅立叶变换的应用简介。
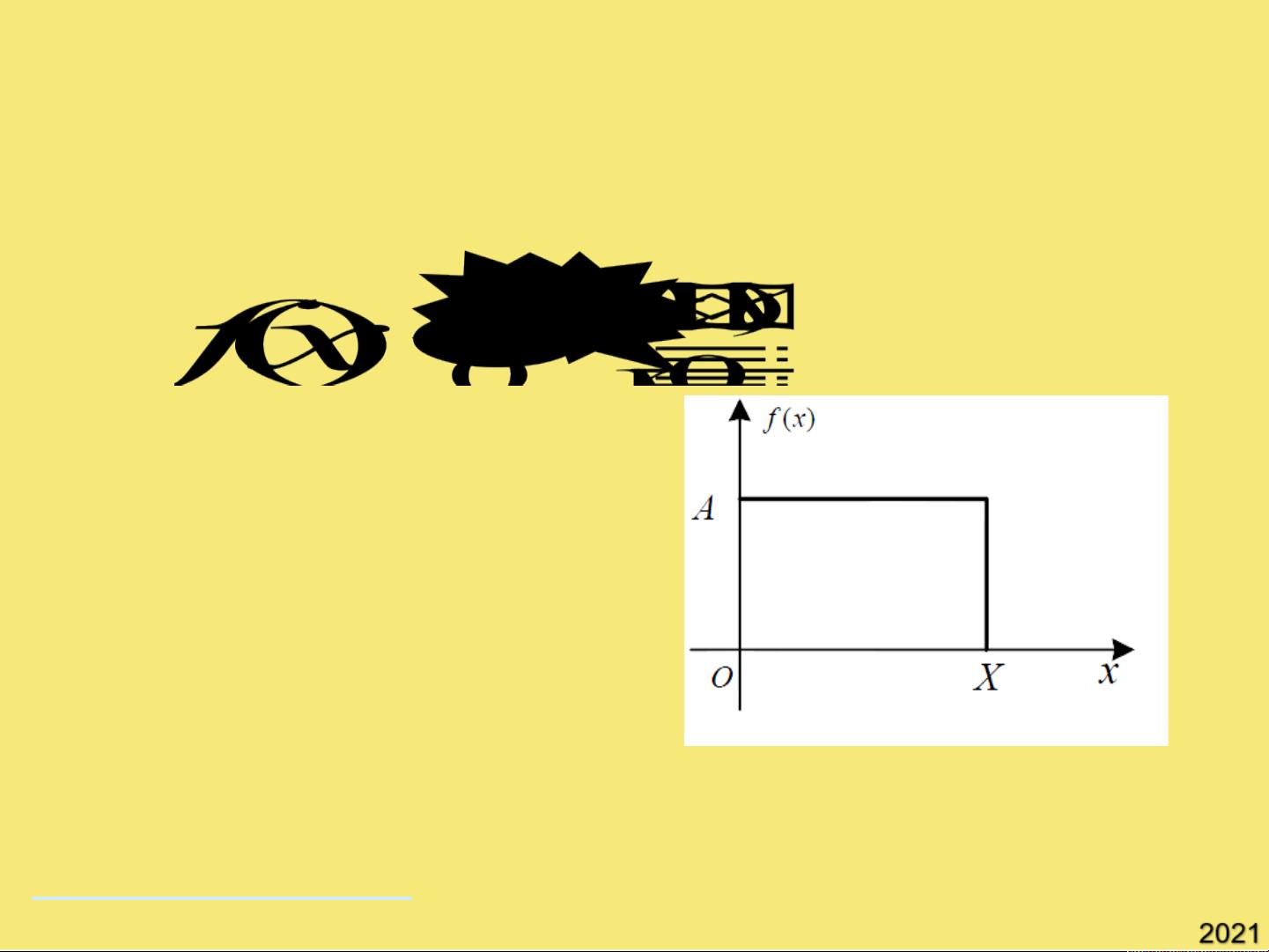
首先,一维傅立叶变换是数学中的一个基本工具,用于将信号或函数从时间域(或空间域)转换到频率域。在图像处理中,这有助于理解和操作图像的频率成分。傅立叶变换定义了一个函数如何由不同频率的正弦和余弦波组成。对于一维连续函数,傅立叶正变换是将函数f(x)转换为傅立叶变换F(u),而傅立叶反变换则是从F(u)恢复原函数f(x)。当函数为实函数时,傅立叶变换可以用复数表示,其傅立叶谱表示了频率成分的幅度,相角反映了各个频率分量的相位,而能量谱则给出了频率分量的强度。
进入二维傅立叶变换领域,这是针对图像处理的核心,因为它能够分析图像的频率特性。二维傅立叶变换将图像f(x, y)转换为频谱F(u, v),这样就可以直接对图像的高频和低频部分进行操作。例如,高频部分通常与图像的细节相关,而低频部分则与图像的全局结构有关。
在MATLAB中,可以使用fft2函数进行二维傅立叶变换,而ifft2函数用于进行二维傅立叶逆变换。这种计算效率高,使得在计算机上对图像进行频率域处理成为可能。MATLAB还提供了可视化工具如fftshift和imagesc来帮助理解变换结果。
傅立叶变换的性质包括线性性、共轭对称性、平移和尺度不变性等,这些性质在处理和分析图像时十分有用。例如,平移不变性意味着傅立叶变换可以揭示图像的周期性特征,而尺度不变性则有助于识别不同大小的图像特征。
最后,傅立叶变换的应用广泛,包括图像滤波、压缩、去噪和增强等。通过在频率域选择合适的滤波器,可以有效地改变图像的空间特性。通常,滤波器的设计和优化在频率域进行,但实际应用往往在空间域完成,这是因为很多滤波操作在MATLAB等软件中可以直接在像素级别实现,更便于硬件实现。
这份资料深入浅出地介绍了傅立叶变换在图像处理中的应用,通过MATLAB的实践操作,不仅能够理论联系实际,还能提升对图像处理中频率域概念的理解和掌握。
相关推荐








黑色的迷迭香
- 粉丝: 808
最新资源
- Android底部导航栏实现教程与示例
- 基于FLD的人脸识别系统_V2版本发布
- React应用的构建与测试入门指南
- MongoDB与Node.js构建电子商务平台功能详解
- 轻狂PDF工具包v1.1.1.0:免费制作与管理PDF的强大软件包
- KodiMm.github.io: 探索我的第一个主机项目
- JS+CSS实现图片列表响应式布局技巧
- STM32控制HC-SR04模块实现超声波测距
- 全面解析SAP JCO3在各操作系统下的版本特性
- Delphi实现的unigui虚拟键盘
- 一步导入IntelliJ IDEA全局设置,简化配置流程
- 探索HTML与GitHub.io的结合运用
- 解决Windows 10 U盘识别问题的官方驱动工具
- 微信风格C#飞机大战游戏开发与改进计划
- 掌握文件编码检测与转码技术
- JavaScript交互式控制台应用:管理任务