电力系统潮流计算解析：牛顿-拉夫逊法与PQ分解法

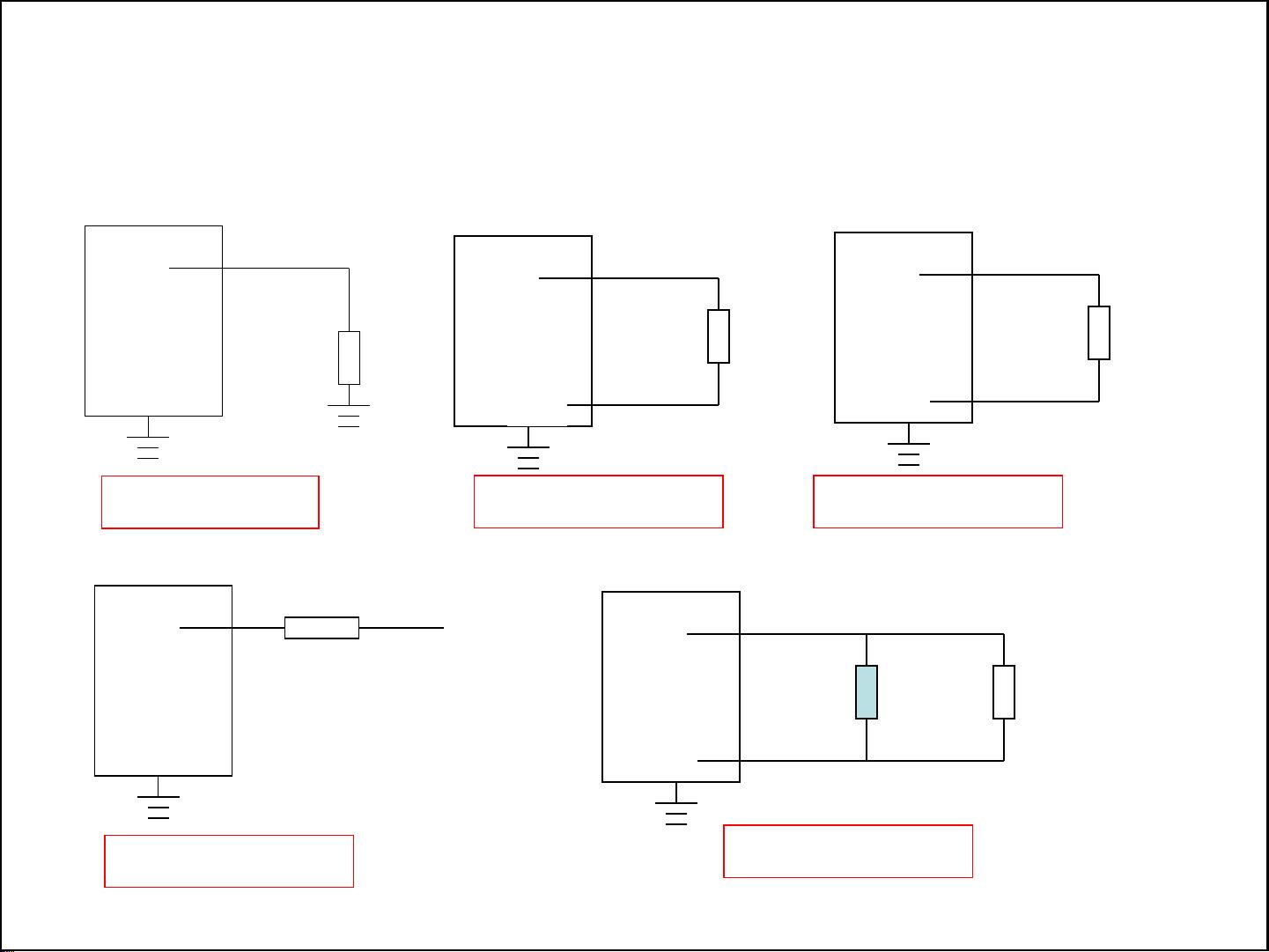
"电力系统的潮流计算相关知识" 电力系统的潮流计算是电力系统分析中的核心部分，主要目的是在给定的运行条件下求解出各节点的电压水平和功率分布。这一过程对于电力系统的规划、扩建、运行方式安排至关重要。潮流计算涉及多个关键知识点： 1. **节点导纳矩阵的形成与修改**：节点导纳矩阵是描述电力系统网络结构的基础，由所有支路的导纳构成。在考虑变压器非标准变比时，需要相应地调整矩阵以反映实际的电气连接。此外，当系统发生变化（如开关状态改变或元件参数更新）时，矩阵也需要进行相应修改。 2. **节点的分类和功率方程**：节点通常分为PV节点（已知电压，求解功率）和PQ节点（已知功率，求解电压）。每个节点根据其特性都有相应的功率平衡方程。 3. **修正方程的形成及雅克比矩阵的计算**：在牛顿-拉夫逊法中，修正方程用于迭代求解非线性潮流问题，雅克比矩阵则是描述系统中各变量之间线性关系的矩阵，其计算直接影响算法的收敛速度和精度。 4. **牛顿-拉夫逊法**：这是最常用的潮流计算方法，通过迭代解决非线性方程组，计算节点电压和功率分布。其优点在于收敛速度快且适应性强，但需要计算雅克比矩阵。 5. **P-Q分解法**：又称快速分解法或FDF（Fast Decoupled Load Flow），它简化了牛顿-拉夫逊法，将电压和功率的计算解耦，特别适用于大规模电力系统的计算，具有更高的效率。 潮流计算的目的不仅包括确定系统的运行状态，还包括评估潜在的过压、过载情况，为继电保护设置提供依据，以及作为稳定性分析和经济运行分析的起点。计算机算法的发展历程从早期的逐次代入法到分块阻抗法，再到牛顿-拉夫逊法和PQ分解法，不断提升了计算速度和准确性。 在实施潮流计算时，选取合适的初始值、有效利用稀疏技术和网络化简技术对于优化计算性能至关重要。例如，选择合理的初始值可以加速算法收敛；利用支路导纳的稀疏性可以减少计算量；网络化简则可降低复杂度，提高计算效率。 电力系统的潮流计算是一个涉及电路理论、非线性方程求解和高效算法的综合问题。随着技术进步，计算方法不断演进，以适应日益复杂和庞大的电力网络需求。