零点分析实操：连续与离散系统稳定性探索

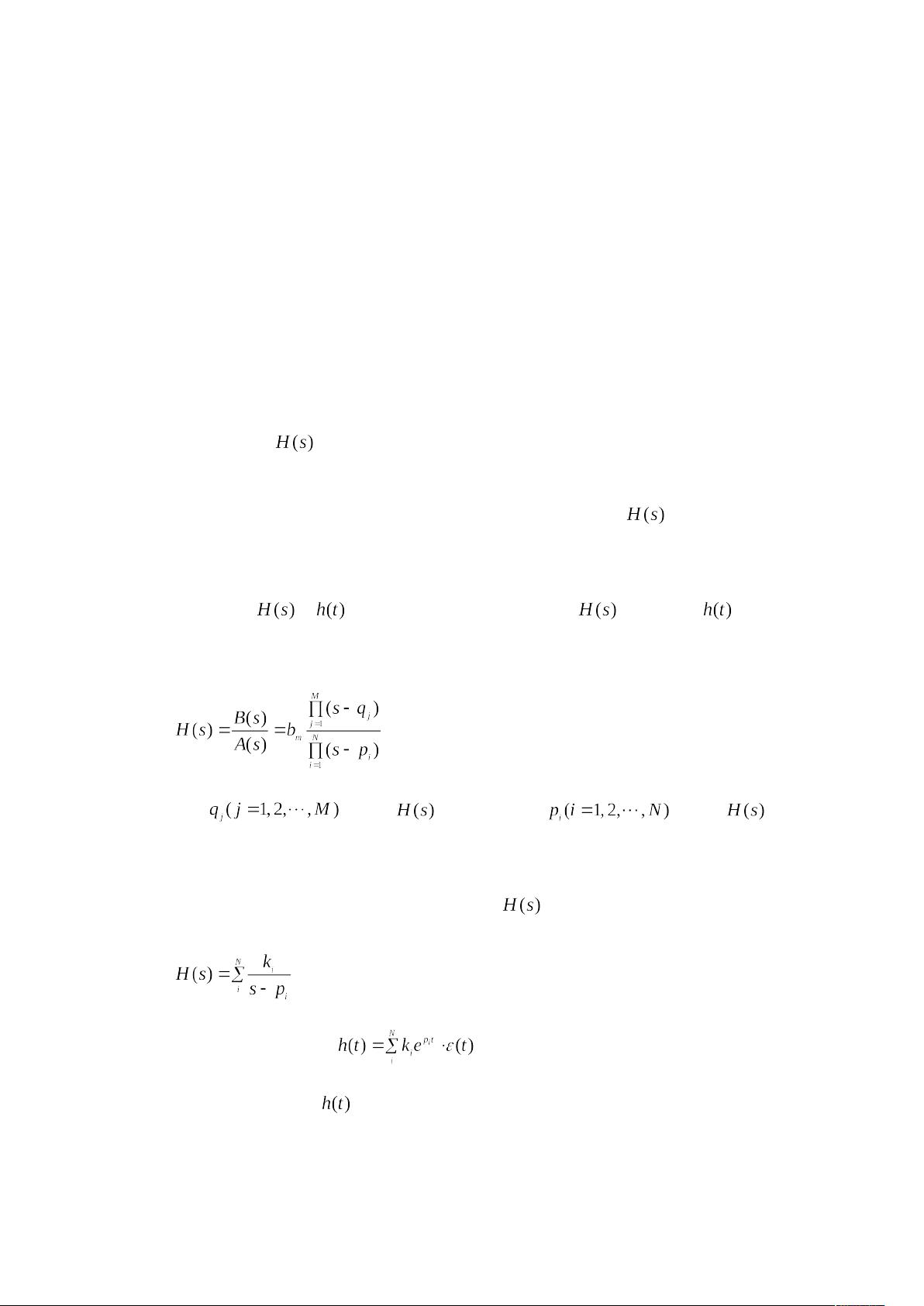
在"克里斯多夫将离开零点分析教程分析"中，主要内容涉及零点和极点分析在连续及离散系统中的重要性。实验目的是深入了解这些概念如何影响系统的动态行为，包括时域响应和频率响应。 首先，零极点分析是研究系统稳定性的一种关键工具。在连续系统中，系统的稳定性取决于系统函数的零点和极点在拉普拉斯域（S平面）上的分布。如果所有极点都在S平面的左半平面，那么系统被认为是稳定的，因为它们对应的冲激响应会随时间衰减。对于低阶系统，可以利用求根公式直接找到极点位置，但高阶系统则需要借助数值计算工具如MATLAB来处理。 在MATLAB中，多项式求根函数`roots()`用于计算系统函数的零极点。例如，给定多项式`134s^2 + 103s + 30 - 4/s`，通过构造系数向量`A`并调用`roots(A)`，我们可以得到该多项式的根，即零点和极点。需要注意的是，系数向量应按照多项式的幂次顺序排列，并可能填充缺失的0。 零极图在分析中起着直观展示的作用，通过绘制在复平面上的零点和极点，可以清晰地看出它们对系统性能的影响。绘制零极图有助于识别系统的特征，如是否存在振荡或增长模式，以及系统响应的动态特性。 离散系统的零极点分析同样重要，尽管分析方法略有不同，但基本原理是相似的，即系统的稳定性、频率响应都受到其零点和极点在Z变换域的影响。通过矢量法，我们可以考察这些点对系统在不同频率下的响应特性。 零点分析是理论与实践相结合的工具，对于理解和设计控制系统的稳定性、性能至关重要。学习和掌握这个概念，不仅可以提升分析和调试复杂系统的能力，还能在实际工程应用中发挥重要作用。无论是理论教学还是实际操作，零点分析都是深入理解控制系统行为的核心内容。