MATLAB实现快速傅立叶分析：信号处理与窗函数应用

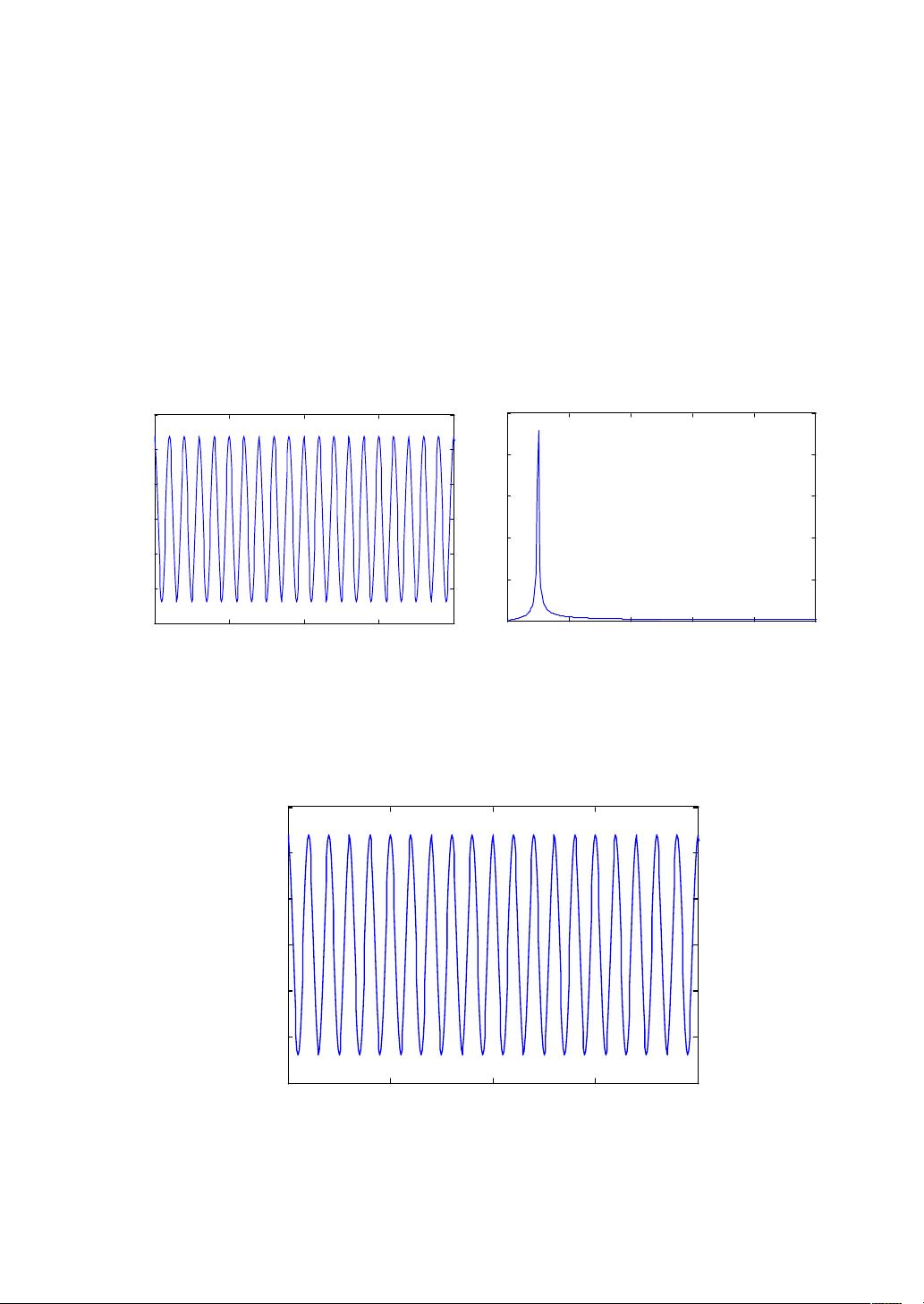
本篇文章《基于MATLAB的快速傅立叶分析程序设计》由作者徐微针对机械工程专业研修生所编写的课程作业，着重介绍了如何利用MATLAB进行信号处理中的快速傅立叶变换（FFT）。作者通过实例讲解了如何对一个人为产生的余弦信号进行功率谱分析，该信号的表达式为x(n)=120.0*COS(2*3.14*SF*n/FS)，其中n=0,1,2,...,N-1，SF代表信号频率，FS是采样频率，固定参数如fs=200Hz，N=512。 文章详细步骤包括： 1. **信号数据与生成**： - 定义了采样频率fs和余弦信号频率sf，生成了时域信号x(n)为120.0*COS(2*3.14*sf*n/fs)。 - 利用MATLAB代码展示了时域波形（图1、2），即余弦函数随时间变化的曲线，以及对应的幅频谱和功率谱密度波形（图2、3）。 2. **信号处理效果对比**： - 分析了未经均值化处理和均值化处理后的信号波形和频谱，发现均值化处理使得波形在时域上有所平移，但频谱保持不变，这有助于理解信号处理对信号特征的影响。 3. **窗函数应用**： - 使用了矩形窗函数和汉明窗函数对信号进行谱分析，分别绘制了时域和频域波形，通过对比展示不同窗函数对频谱估计的影响，这有助于了解窗函数选择对频谱估计精度和特性的影响。 4. **典型函数的频谱分析**： - 提供了对其他窗口函数如汉宁窗和三角窗函数的频谱分析，进一步展示了各种窗函数对信号处理的不同效果。 5. **整周期与非整周期分析**： - 对于整周期和非整周期信号的处理进行了区分，这对于理解和解释信号的周期性以及在实际应用中的处理策略至关重要。 这篇文章提供了实用的MATLAB编程示例，展示了如何通过傅立叶变换技术对信号进行深入分析，对信号处理初学者和工程师来说是一份宝贵的参考资料。通过本文，读者可以掌握傅立叶变换的基本概念和MATLAB编程技巧，应用于实际的信号处理问题中。