FPGA上的CORDIC算法：高效实现三角函数与超越函数

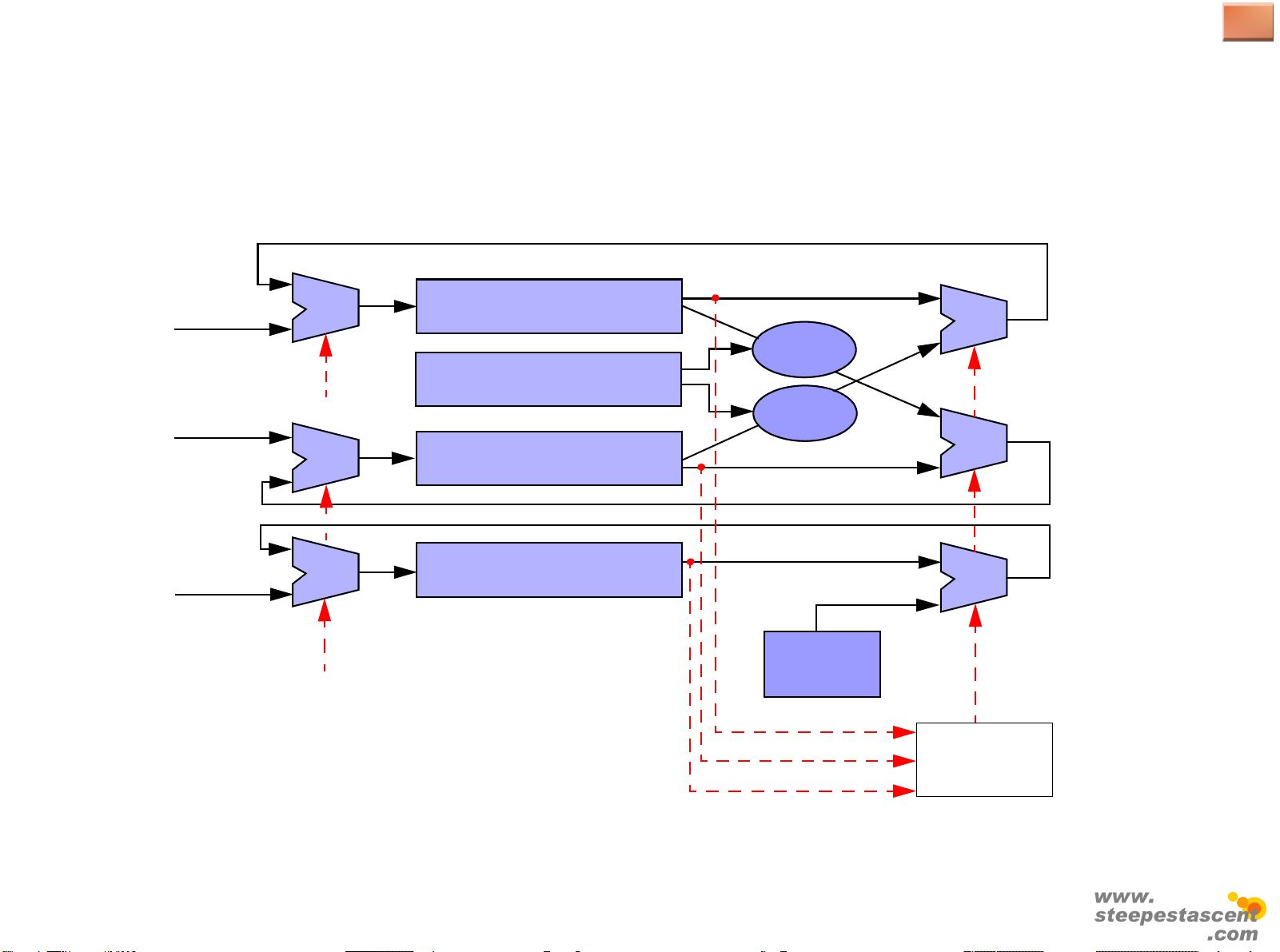
"CORDIC算法是用于在硬件中高效计算三角函数和相关数学操作的一种迭代算法。它最初由J. Volder在1957年提出，适用于早期计算能力有限的环境，现在广泛应用于FPGA（现场可编程门阵列）设计，特别是在数字信号处理(DSP)领域。" CORDIC（坐标旋转数字计算机）算法基于简单的加法、减法和位移操作，不需要乘法器或除法器，这使得它非常适合于硬件实现，尤其是在资源有限的FPGA中。该算法主要用于计算以下函数： 1. 正弦(sine)和余弦(cosine)：通过迭代调整坐标系统，CORDIC可以计算出给定角度的正弦和余弦值。 2. 正切(tangent)：同样通过迭代过程，可以得到角度的正切值。 3. 逆正切(atan)：通过CORDIC算法可以求解角度，当已知正切值时。 4. 对数(logarithm)和除法：CORDIC还可以扩展到计算自然对数和除法。 5. 平方根(root extraction)：在某些实现中，可以通过CORDIC计算平方根。 CORDIC算法的基本工作原理如下： - 它使用一系列固定角度（通常是二进制反码表示的Gold Code序列），每次迭代中，根据当前矢量的方向调整坐标轴。 - 每次迭代，通过位移操作增减矢量的X和Y分量，根据当前角度和前一迭代的残差来决定位移方向。 - 迭代次数取决于所需的精度，更多的迭代提供更精确的结果。 - 最终，X分量通常对应于正切值，而Y分量可用于计算其他函数，如余弦或对数。 参考文献中提供了更多关于CORDIC算法的详细信息： 1. R. Andraka的综述文章提供了CORDIC算法在FPGA应用中的概述。 2. BYU的EE621课程资料详细介绍了CORDIC算法的运作机制。 3. CORDIC教程网站提供了易于理解的解释和示例。 4. M.J. Irwin的《计算机算术》一书中详细讨论了CORDIC在计算中的应用。 由于其高效性和硬件友好性，CORDIC算法在20世纪70年代开始被Hewlett-Packard等公司的手持计算器采用，并且至今仍然是数字信号处理和嵌入式系统中的一个重要工具。尽管现代处理器和硬件中有更强大的数学库，但在资源受限的环境中，如FPGA设计，CORDIC仍然是一个值得考虑的选择。