验证时频采样理论：1kHz vs 300Hz vs 200Hz信号处理与恢复

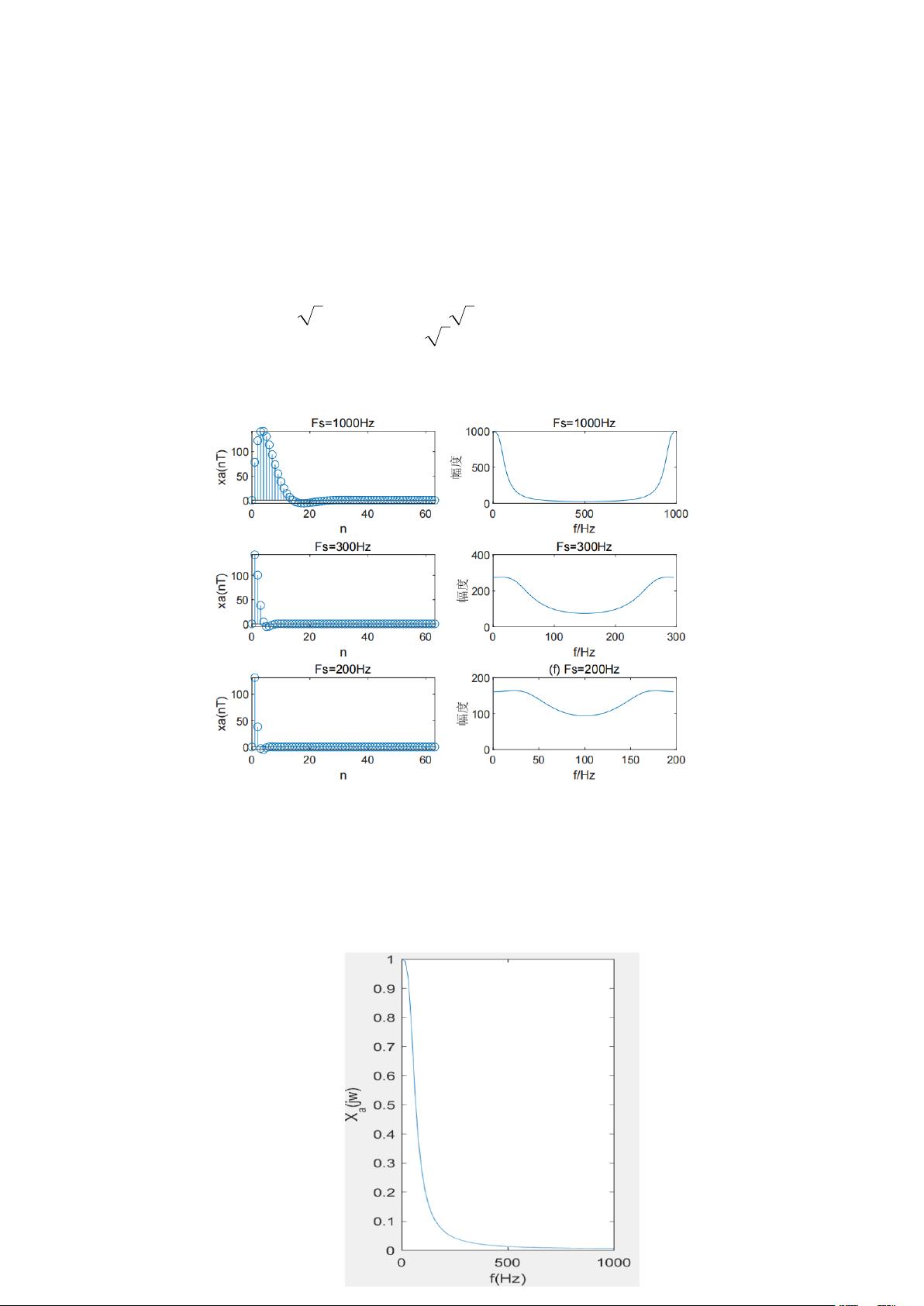
本实验主要围绕数字信号处理中的时域采样和频域采样展开，涉及到的关键知识点包括： 1. **时域采样定理**：实验首先验证了时域采样定理，即对于模拟信号 \( x(t) = A\sin(\omega t - \alpha) \)，采样频率 \( F_s \) 必须至少等于信号最高频率 \( \frac{2\pi}{T_p} \)（在本例中为 \( \frac{2\pi}{50ms} \) 或者 \( 1000 \) Hz）以防止频谱混叠。通过采样频率 \( F_s = 1kHz, 300Hz, 200Hz \) 分别对信号进行采样，实验结果显示，当 \( F_s = 1kHz \) 时频谱混叠较小，随着采样频率降低，混叠现象加剧。 **基础要求**： - 生成了不同采样频率下的序列 \( x_1(n), x_2(n), x_3(n) \)，并在时域绘制了波形，同时对频域的幅频特性进行了分析，展示了不同采样频率下频谱分布的变化。 **创新挑战**： - 实验还挑战了信号的插值恢复，当采样频率足够高时，插值恢复的信号质量较好，能够接近原始信号。 - 通过比较不同采样点数下的频域恢复结果，强调了频域采样定理的重要性，即当 \( N \geq M \) 时，不会发生混叠失真，而 \( N < M \) 时会出现失真。 2. **频域采样定理**： - 验证了频域采样的概念，即当对信号的频谱函数在时域进行周期延拓后，采样点数 \( N \) 足够大（大于信号长度 \( M \)），则可以得到无失真的主值区间序列。 - 当 \( N < M \) 时，会发生时域混叠失真，这在实验中通过 \( N = 8 \) 和 \( N = 16 \) 的对比得到了体现。 **创新挑战**： - 显示了不满足频域采样定理（如 \( N = 8 \)）的情况下，恢复的信号与原信号不匹配；而在满足条件（如 \( N = 16 \)）时，可以正确恢复原始信号。 此外，实验还提供了 MATLAB 代码片段，展示了如何使用 FFT 进行采样和频谱分析，包括初始化参数、计算抽样点、执行 FFT 变换以及绘制时域波形和频谱图。 总结来说，这个实验让学生深入理解了时域和频域采样理论在实际应用中的作用，并通过实验操作练习了信号处理技术，特别是如何利用采样定理来确保信号质量和避免失真。