MATLAB回归分析实战：建立与解读经验公式

MATLAB数据分析方法中的回归分析是本章核心内容，它是统计学中一种强大的工具，用于探索自变量与因变量之间的关系，并构建预测模型。本章首先介绍了基本的一元回归模型，包括一元线性回归的概念和原理。 一元线性回归模型是基于最小二乘法，假设因变量Y受自变量x的影响，并存在随机误差项，满足线性关系 \( Y = \beta_0 + \beta_1 x + \epsilon \)，其中\(\beta_0\)为截距，\(\beta_1\)为斜率。通过样本观测值，我们使用\( \hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x} \)和\( \hat{\beta}_1 = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (x_i - \bar{x})^2} \)分别估计回归系数。回归分析的主要任务包括估计参数、检验线性关系的显著性以及在特定自变量值下的预测。 在实际应用中，例如案例中的社会商品零售总额与职工工资总额的数据分析，通过MATLAB代码，我们首先导入数据，绘制散点图以观察两者的关系，然后通过计算相关系数和回归参数（如b1=2.7991，b0=-23.5493）建立经验公式。回归模型可以用来预测当职工工资总额为0时的社会商品零售总额，即约-23.55亿元。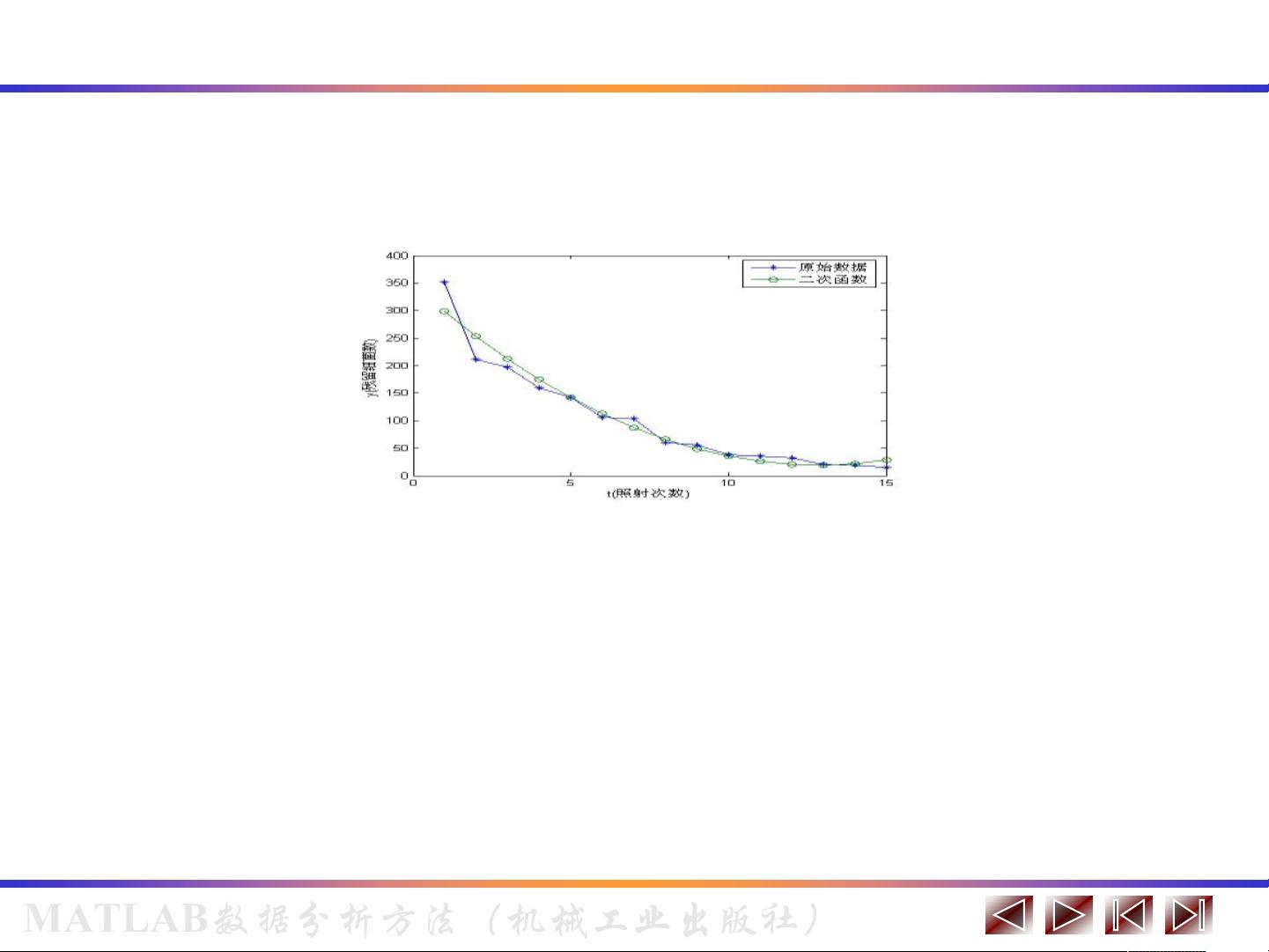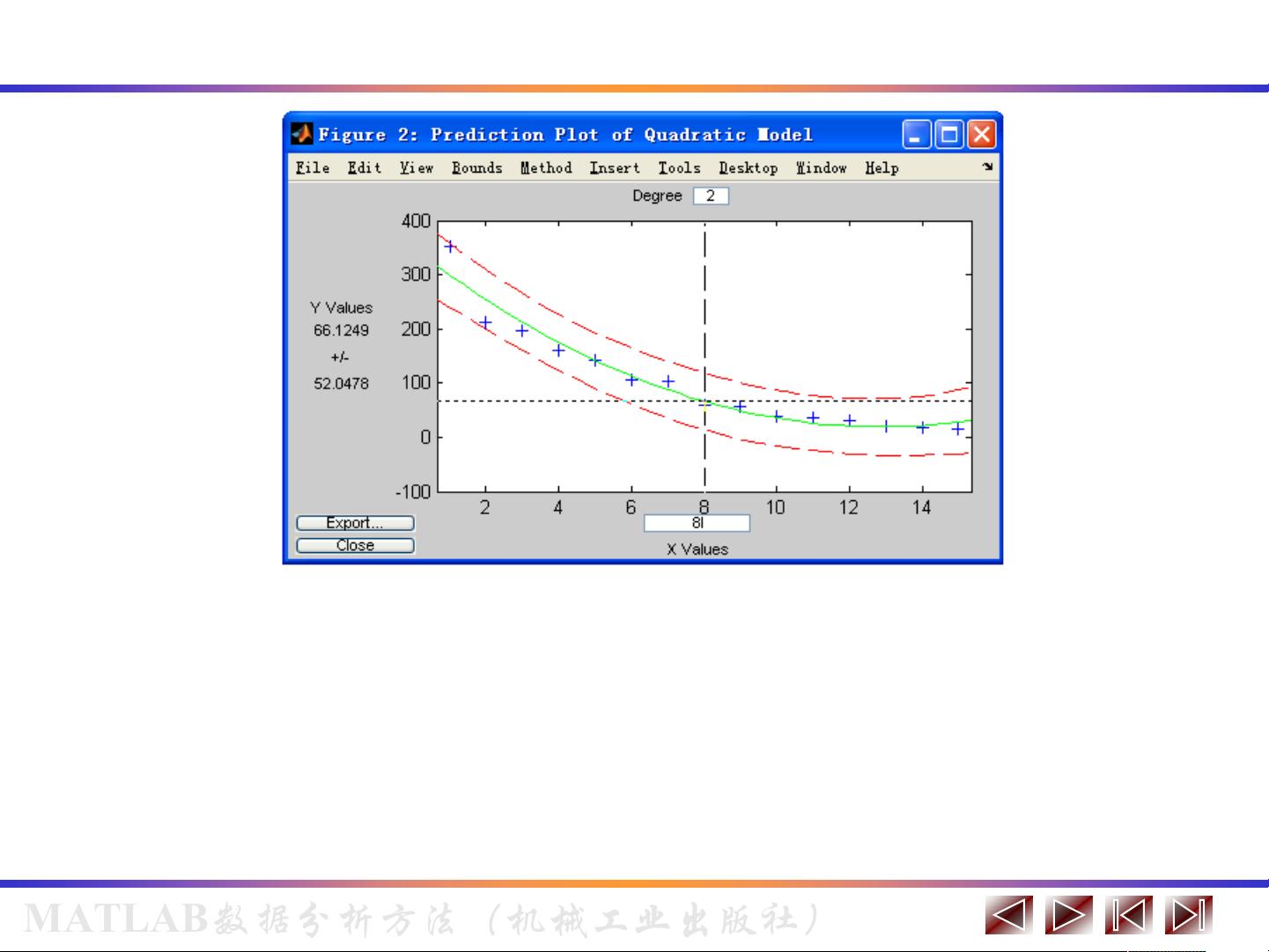 对于一元多项式回归模型，它扩展了一元线性回归，允许因变量与自变量的关系是非线性的，通过多项式函数来拟合数据。这在数据呈现复杂趋势时非常有用。在MATLAB中，可以使用polyfit函数来拟合多项式回归模型。 在本章中，不仅介绍了理论概念，还提供了具体的MATLAB操作步骤，确保了学习者能够逐步掌握回归分析的实践应用。无论是初学者还是有一定基础的学习者，都可以通过本章的内容深化对MATLAB在数据分析中的运用理解。全套课程内容丰富，涵盖了从基础到进阶的多个数据分析方法，适合全面提升MATLAB数据分析能力。