图论网络模型探索：最短路径、最小生成树与最大流问题

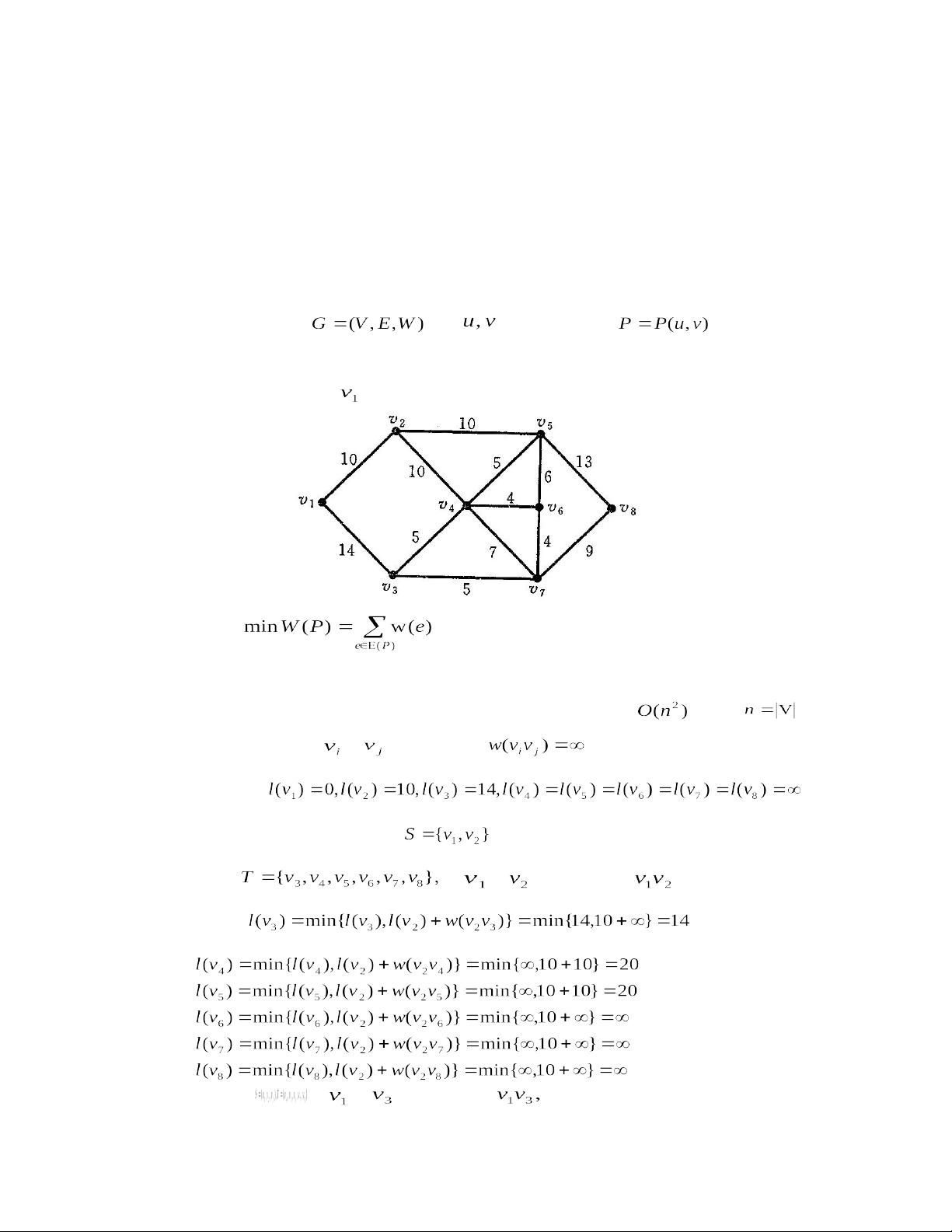
"图论与网络模型" 图论与网络模型是数学和计算机科学中的核心概念，广泛应用于数据结构、算法设计以及优化问题。本部分主要涉及最短路径、最小生成树和网络最大流三个关键问题。 一、最短路径 最短路径问题是在加权图中寻找两个指定顶点间权值之和最小的路径。Dijkstra算法是最常用的求解两点间最短路径的方法，时间复杂度为O(E log V)，适用于无负权边的图。Floyd算法则可以求解任意两点间的最短路径，时间复杂度为O(V^3)，适用于所有类型的图。这些算法在实际中有多种应用场景，如交通路线规划、工程项目的进度管理等。 二、最小生成树 最小生成树问题是在加权连通图中找到一个边权重之和最小的树，涵盖所有顶点。Kruskal和Prim算法是解决这一问题的常用方法，它们的时间复杂度均为O(E log V)。最小生成树在电路设计、网络连接优化等领域有重要应用。 三、网络最大流问题 网络最大流问题是寻找在具有容量限制的图中，从单一源点到单一汇点的最大流量。Ford-Fulkerson算法是基础，而Edmonds-Karp算法在效率上有优化，其时间复杂度为O(VE^2)。单纯形法虽非多项式时间，但在某些特定情况下仍能有效解决问题。网络最大流的应用包括运输问题、资源分配以及网络设计等。 四、图的独立集、覆盖集与支配集问题 这部分虽然未详述，但通常涉及图的组合优化问题。独立集是图中没有边相连的一组顶点，覆盖集是指最少的顶点数能覆盖所有边，支配集则是能"控制"整个图的最小顶点集。这些问题在图的染色、社区检测、网络分析等领域有重要作用。 以上内容涵盖了图论与网络模型的基础理论和算法，它们是解决复杂优化问题的重要工具，并在实际问题中展现出极大的实用价值。通过深入理解和掌握这些知识，能够帮助我们在实际工程和科研中设计出更高效、更优化的解决方案。