深度学习基础:卷积神经网络中的互相关运算与卷积层解析
需积分: 0 190 浏览量
更新于2024-08-29
收藏 355KB PDF 举报
"Day5 - 介绍卷积神经网络的基础知识,包括二维互相关运算和卷积层,以及填充和步幅的概念"
卷积神经网络(Convolutional Neural Networks,CNN)是深度学习领域中用于图像识别和处理的核心技术。本节主要探讨其基本构成和运算原理。
1、二维互相关运算与卷积层
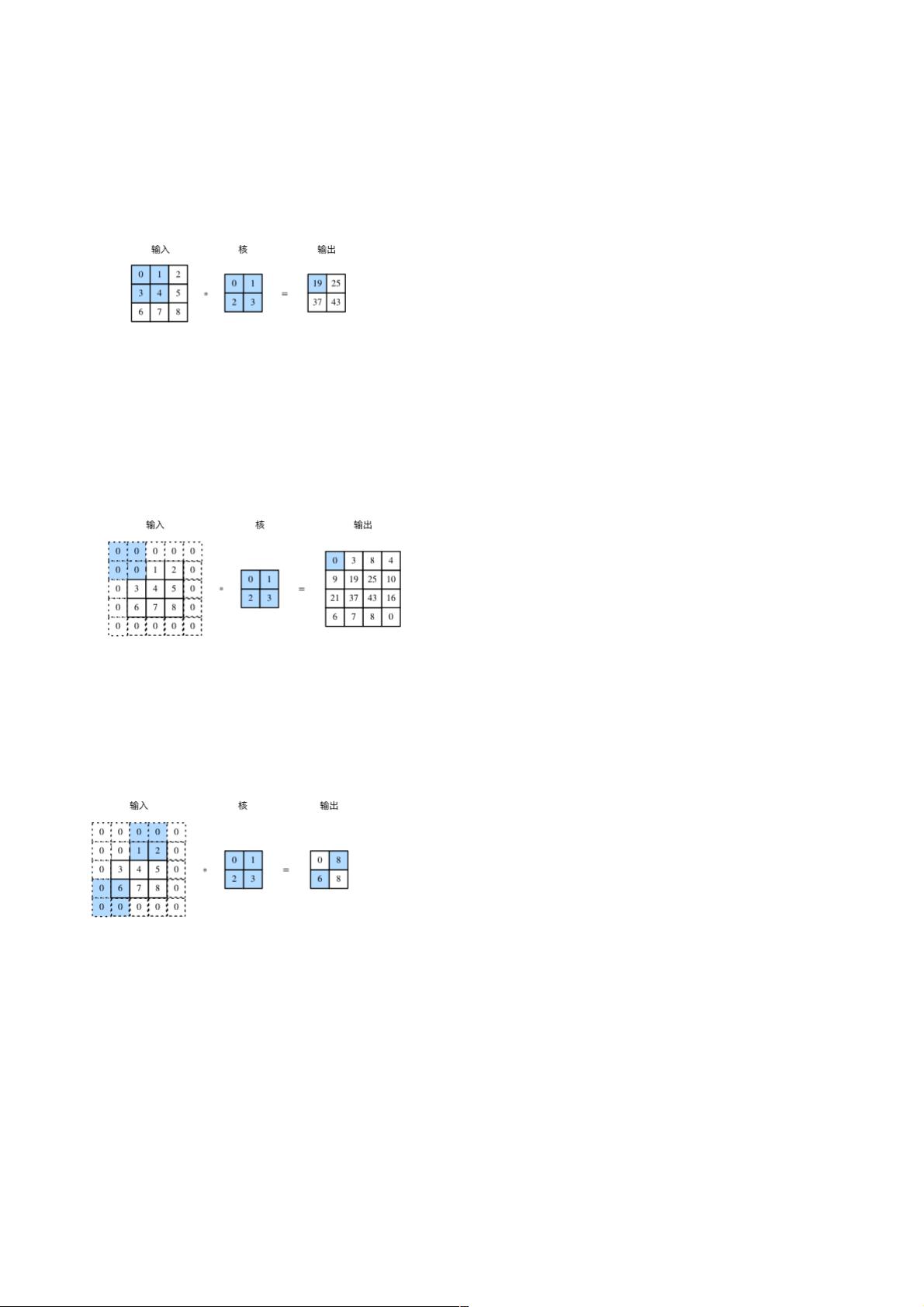
二维互相关运算是一种在图像处理和神经网络中广泛使用的操作。它涉及到两个数组:一个二维输入数组(通常是图像数据)和一个二维核(或称卷积核、过滤器)。卷积核在输入数组上滑动,对每个位置的输入子数组与卷积核进行逐元素相乘并求和,结果存储在输出数组的相应位置。这种运算方式有助于捕捉输入数据中的局部特征。
卷积层是构建CNN的基本单元,它通过应用二维互相关运算来提取输入数据的特征。卷积层的输出不仅包含互相关运算的结果,还加入了一个标量偏置,使得模型能够学习更复杂的模式。尽管术语“卷积”常被用来描述这种运算,但实际上卷积层使用的是互相关运算,因为卷积核是可学习的,所以互相关与卷积的区别可以忽略不计。
2、填充和步幅
填充(padding)是为了保持输出尺寸不变或者调整输出尺寸而对输入边缘添加额外元素(通常是0)。例如,对于3x3的卷积核,若设置合适的填充,可以在步幅为1的情况下保持输入和输出的尺寸相同。填充可以帮助捕捉边界信息,避免特征检测仅集中在输入的中心部分。
步幅(stride)决定了卷积核在输入上移动的步长。步幅越大,输出的尺寸越小,模型捕捉的局部特征数量减少,但计算效率提高。反之,步幅越小,输出尺寸越大,模型能够捕获更多细节,但计算量增加。通常,步幅为1意味着卷积核在每个位置都会进行一次运算。
综合填充和步幅,可以灵活地控制输出形状,以适应不同的应用场景和性能需求。例如,当填充等于卷积核大小减1时,输出形状简化为输入形状除以步幅。如果输入尺寸能被步幅整除,输出形状则直接是输入形状除以步幅的整数值。
总结来说,卷积神经网络通过卷积层的互相关运算、适当的填充和步幅来提取图像数据的特征,这些基础概念是理解和构建CNN模型的关键。了解这些原理后,我们可以进一步探索池化层、激活函数、全连接层等CNN的其他组成部分,以及如何优化和训练这些网络以解决实际问题。
点击了解资源详情
点击了解资源详情
点击了解资源详情
weixin_38669618
- 粉丝: 7
- 资源: 912
最新资源
- Java毕业设计项目:校园二手交易网站开发指南
- Blaseball Plus插件开发与构建教程
- Deno Express:模仿Node.js Express的Deno Web服务器解决方案
- coc-snippets: 强化coc.nvim代码片段体验
- Java面向对象编程语言特性解析与学生信息管理系统开发
- 掌握Java实现硬盘链接技术:LinkDisks深度解析
- 基于Springboot和Vue的Java网盘系统开发
- jMonkeyEngine3 SDK:Netbeans集成的3D应用开发利器
- Python家庭作业指南与实践技巧
- Java企业级Web项目实践指南
- Eureka注册中心与Go客户端使用指南
- TsinghuaNet客户端:跨平台校园网联网解决方案
- 掌握lazycsv:C++中高效解析CSV文件的单头库
- FSDAF遥感影像时空融合python实现教程
- Envato Markets分析工具扩展:监控销售与评论
- Kotlin实现NumPy绑定:提升数组数据处理性能