直角三角形与二次函数探索：存在性问题解析

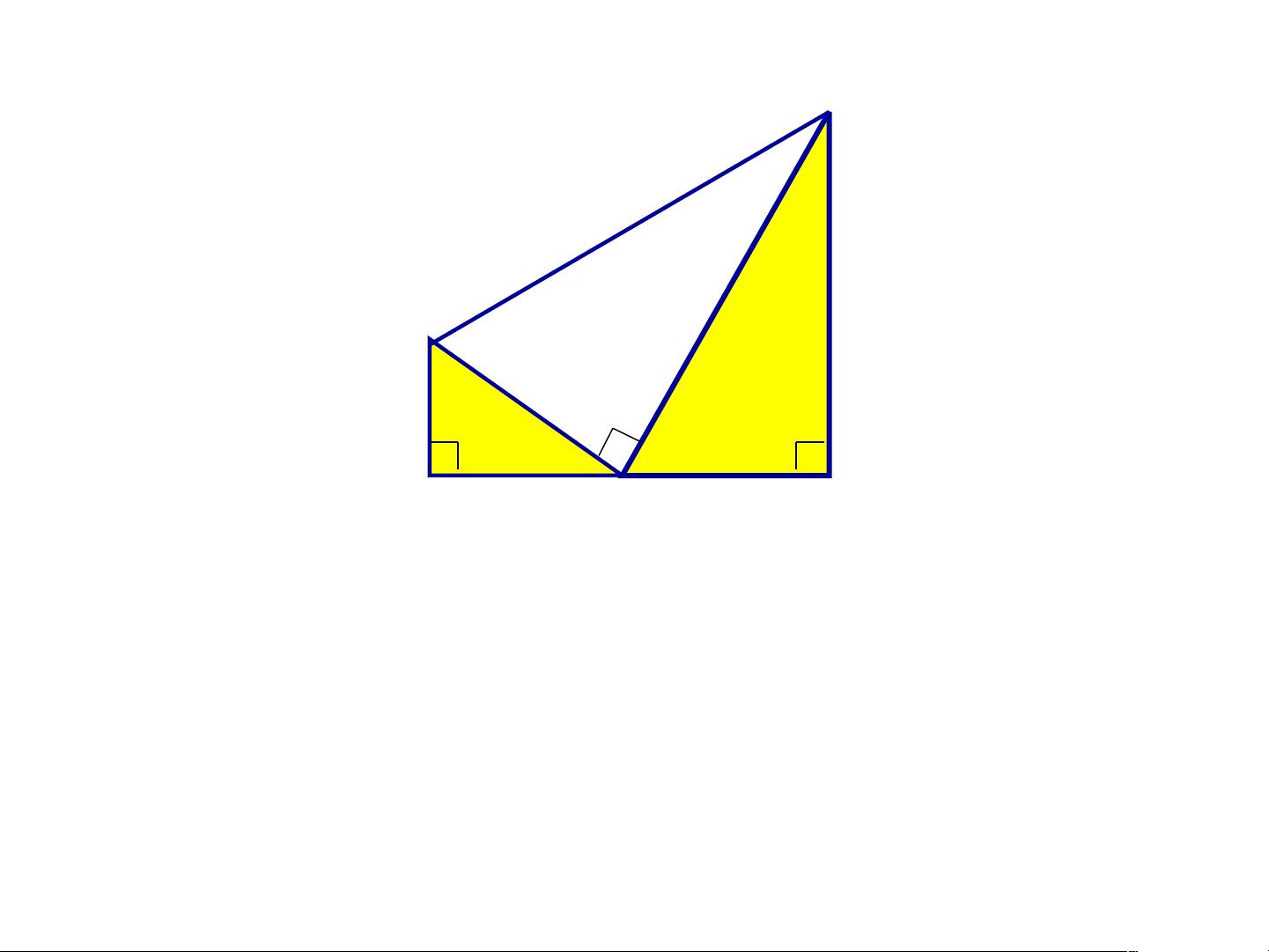
"该资源是一份关于二次函数与直角三角形的专题课件，包含教育精品内容，探讨了直角三角形的存在性问题、射影定理、K型图的应用以及直角三角形斜边上的中线等知识点。通过不同情境的几何问题，引导学生掌握如何解直角三角形的存在性问题，包括点在直线或抛物线上的问题。课件还提供了多个自学指导环节，让学生练习求解直角三角形中点的坐标，以及判断在特定直线或位置上是否存在使三角形成为直角三角形的点。" 课件详细讲解了以下知识点： 1. **直角三角形的存在性问题**：在给定的动点问题中，点M和N分别从O和B出发，研究它们运动过程中形成的△AQM的面积S与时间t的关系。这涉及到动态几何中的函数关系建立和最值问题，需要理解点的位置变化如何影响图形的性质。 2. **射影定理**：通过相似三角形的性质，推导出直角三角形斜边上的高与边长之间的比例关系，即AC² = AD * AB，BC² = BD * BA，DC² = DA * DB。这些公式在解决涉及直角三角形的问题时非常有用。 3. **K型图与相似三角形**：利用相似三角形的性质证明BD·BE = AD·CE，这是解决直角三角形问题时的一种常见方法，通过构建K型图来简化问题。 4. **直角三角形斜边上的中线**：介绍直角三角形斜边中线的性质，即它等于斜边的一半，这一特性在求解几何问题时可作为重要依据。 5. **点在坐标轴上的直角三角形问题**：通过设定点P在x轴或特定直线上，探究当△AOP为直角三角形时，点P的坐标。这需要学生熟悉坐标系中的几何关系，并能够将几何问题转化为代数方程求解。 课件还设置了多种情况的自学检测，如在直线x=3或x=0.5上寻找使△PAC为直角三角形的点P，通过这些练习，帮助学生巩固所学知识并提升问题解决能力。 这份课件全面深入地探讨了二次函数与直角三角形的结合，不仅教授了基本理论，还提供了丰富的实践应用，是学习和掌握这个主题的宝贵资源。