信息论习题解析：后处理不影响互信息，信道并行组合容量公式

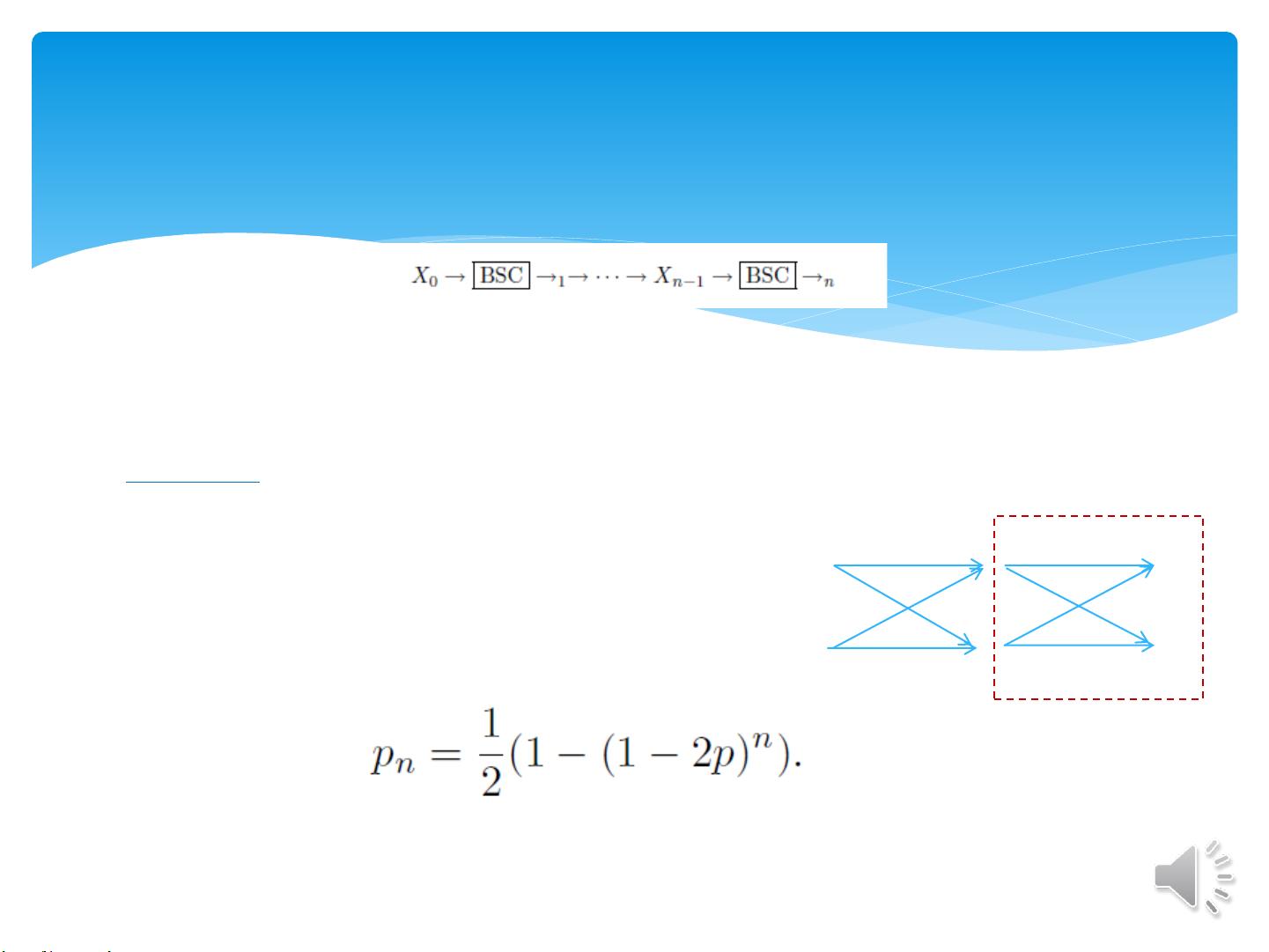
本资源主要聚焦于IT行业的信息论部分，特别是针对信号传输与处理的理论基础进行深入探讨。第七章习题选解涵盖了多个关键概念，包括互信息量的提升、信道容量的计算、并行信道组合、串联BSC信道的Shannon容量以及时变离散无记忆信道。 1. 互信息量提升 - 习题7.1指出，对接收分组实施后处理并不能提升互信息量。这是基于数据处理不等式，表明对数据进行处理不会增加原始信号之间的信息含量，因此接收端的处理操作对总的信道容量没有直接影响。 2. 信道容量计算 - 习题7.5涉及两个信道的并行组合，其总容量等于各自信道容量之和，即C = C1 + C2，这是因为并行信道中的每个信道独立工作，接收端可以独立处理各自的输入，互信息量I((x1,x2);(y1,y2)) 分别计算后相加得到总容量。 3. 串联BSC信道 - 习题7.7要求计算串联BSC信道的Shannon容量，通过递归分解，利用pn表示串联信道的等效差错概率，找出pn的计算公式。这个问题的关键在于理解如何将串联信道的输出概率与输入概率关系转化为递归关系。 4. 时变信道 - 习题7.11探讨的是时变离散无记忆信道，其中互信息量I(y1,…,yn; x1,…,xn)的计算是关键，因为时变特性导致每个时间步的转移概率不同。最大互信息量与输入概率分布p(xn)有关，通过求解p(xn)使得互信息量最大化，从而定义平均容量C。 这些习题选解旨在帮助读者理解和掌握信息论中的核心概念，包括信道容量的加法性质、概率链规则以及如何处理不同类型的信道模型。通过解决这些问题，学习者能够深化对信息理论在实际通信系统中的应用的理解。