DAMASK：多物理场晶体塑性模拟工具

需积分: 36 142 浏览量更新于2024-07-09 1 收藏 29.86MB PDF 举报

"DAMASK (Düsseldorf Advanced Material Simulation Kit) 是一款强大的多物理场建模工具，专门用于模拟从单晶到组件级别的晶体塑性、热效应以及损伤现象。这款软件包旨在处理复杂的材料科学问题，涵盖了从微观尺度到宏观尺度的各种力学行为。" 在晶体塑性这一领域，DAMASK 提供了高级的模拟框架，能够精确地描述金属和其他晶体材料在受力情况下的形变行为。晶体塑性涉及晶体内部位错的运动与交互，这些位错是材料塑性变形的主要机制。DAMASK 可以捕捉这些复杂的位错动力学过程，包括位错生成、传播、交互和湮灭，以及它们对材料性能的影响。此外，DAMASK 还考虑了热效应，这对于理解材料在加热或冷却过程中的行为至关重要。热效应可能改变材料的晶体结构，影响其机械性能，并可能导致相变。通过集成热模型，DAMASK 能够模拟温度变化如何影响位错行为和材料的塑性响应。在组件级别，DAMASK 可以应用于大型结构部件的模拟，如发动机部件或航空航天结构，这些部件可能承受各种载荷并经历广泛的温度变化。这种跨尺度建模能力使得工程师能够在设计阶段就预测和优化材料的性能，减少实验成本并提升产品寿命。 DAMASK 的开发团队由多个机构的专家组成，包括德国马克斯·普朗克钢铁研究所、曼彻斯特大学材料学院、密歇根州立大学化学工程与材料科学学院等。这表明该软件包是国际合作和跨学科研究的产物，结合了材料科学、计算力学和工程学的最新研究成果。软件的广泛应用包括但不限于以下几个方面： 1. **材料设计**：通过对材料的微观结构和力学性能进行预测，帮助研发新型高强度、高耐久性的材料。 2. **工艺优化**：评估和改进制造过程，如锻造、轧制或焊接，以减少缺陷并提高产品质量。 3. **失效分析**：模拟和预测材料在极端条件下的失效模式，从而预防实际应用中的故障。 4. **安全性评估**：在核电站、飞机或汽车等关键领域的组件设计中，确保其在预期工作环境下的可靠性。 DAMASK 是一个全面的多物理场模拟工具，它通过模拟晶体塑性、热效应和损伤现象，为材料科学家和工程师提供了强大的研究和设计平台，以应对从微观到宏观的复杂材料挑战。

= ×

( )

M n F ,

g g g( ) ( ) ( )T

(33)

where

g( )T

corresponds to the jump, i.e. diﬀerence, in the

deformation gradient between constituent g and its neighbor across

an interface

. By correlating the incompatibility with a density of

accommodating “geometrically necessary” dislocations, a surface

energy function is proposed that penalizes the incompatibility at

interface

of constituent g:

b µ

c M

sinh( ),

g g

g( )

( ) ( )

( )

(34)

where

g( )

denotes the isotropic equivalent shear modulus of a possibly

anisotropic constituent g [122],

g( )

the magnitude of the B

URGERS vector

of the dislocations and

g( )

the magnitude of the mismatch. Two

dimensionless scalars are introduced in Eq. (34):

sets the eﬀective

weight of the penalty function, and c controls the over-proportionality

of the penalty function with respect to the mismatch magnitude, such

that Eq. (34) shows a linear behavior if

c 0

. Setting

= 0

renders the

model “penalty-free”, i.e. incompatibility between neighboring

constituents is tolerated, whereas

results in a very strong

penalty function which imposes a “fully compatible” deformation

mode. The overall mismatch penalty density (per unit reference

volume)

is computed as the volumetric average of the penalties at

all interfaces of all constituents, i.e.

= =

( )

(35)

4.1.3.3. Energy minimization. The deformation energy (or mechanical

work) density of constituent g per unit reference volume at time t,

denoted by

g( )

, is given by

= P F( )· ( ) d ,

( )

(36)

where

= tF F /

( )

is the rate of the deformation gradient. The overall

work density of the cluster,

, can be obtained as the volumetric

average of the work density of all constituents as

g g

( ) ( )

(37)

In the RGC model, all relaxation vectors

g( )

are determined such that

the total energy density (including the mismatch penalty) of the cluster

is minimum for a given

, i.e.

= +a a aargmin{ ( ) ( )}

g g g( ) ( ) ( )

Assuming convexity of the total energy density

, the solution

of the energy minimization problem is equivalent to the stationary

point,

+ =a 0( )/

g( )

, for each interface of constituent g.

Evaluating the above derivatives, the solution of the energy

minimization leads to the following balance of traction (or

equilibrium condition) at each interface

of constituent g:

+ + =P R n P R n 0( ) ( ) ,

g g

( ) ( ) ( ) ( )

( )

(38)

where

denotes the constituent opposite to g across the interface . In

the above equilibrium condition,

g( )

represents a tensor analogous to

the ﬁrst P

IOLA–KIRCHHOFF stress tensor obtained as the derivative of the

total mismatch penalty with respect to the constituent deformation

gradient, i.e.

=R F/

g g( ) ( )

. A more detailed discussion on the “penalty

stress” tensor

g( )

can be found in [105].

4.2. Thermal ﬁelds

The average temperature ﬁeld

acting on a material point is par-

titioned onto the

constituents

= …g N1, ,

such that

T T .

g g

( ) ( )

(39)

An iso-ﬁeld homogenization assumption is used, whereby the

equality of the temperature ﬁeld

g( )

of each constituent g with the

average temperature ﬁeld

is enforced:

= = …T T g N, 1, , .

g( )

(40)

Typically, a diﬀerent ﬂux

g( )

and driving force

g( )

results in each

constituent g, which can, for instance, be due to anisotropy or diﬀerent

constitutive behavior. The ﬂux and driving force at the material point

are calculated as the average of all constituents:

f f

( )

(41a)

f f .

( )

(41b)

4.3. Damage ﬁelds

Similar to the partitioning of

given in Eq. (39), the average da-

mage ﬁeld

acting on a material point is partitioned onto the

constituents

= …g N1, ,

such that

g g

( ) ( )

(42)

As for the temperature (Eq. (40)), the iso-ﬁeld homogenization as-

sumption is used, whereby the equality of the damage ﬁeld

g( )

of each

constituent g with the average damage ﬁeld

is enforced:

Fig. 2. Example of a

× ×4 5 3

cluster considered by the Relaxed Grain Cluster

(RGC) scheme. The diﬀerent gray shades indicate diﬀerent crystallographic

orientations and/or phases of the constituents (“grains”). Figure adopted from

[16] with permission from John Wiley and Sons.

Fig. 3. Illustration of the relaxation vectors of constituent (“grain”) g. Figure

adopted from [105,112,116] with permission from Springer Nature.

F. Roters et al.

Computational Materials Science 158 (2019) 420–478

429

= = …g N, 1, , .

g( )

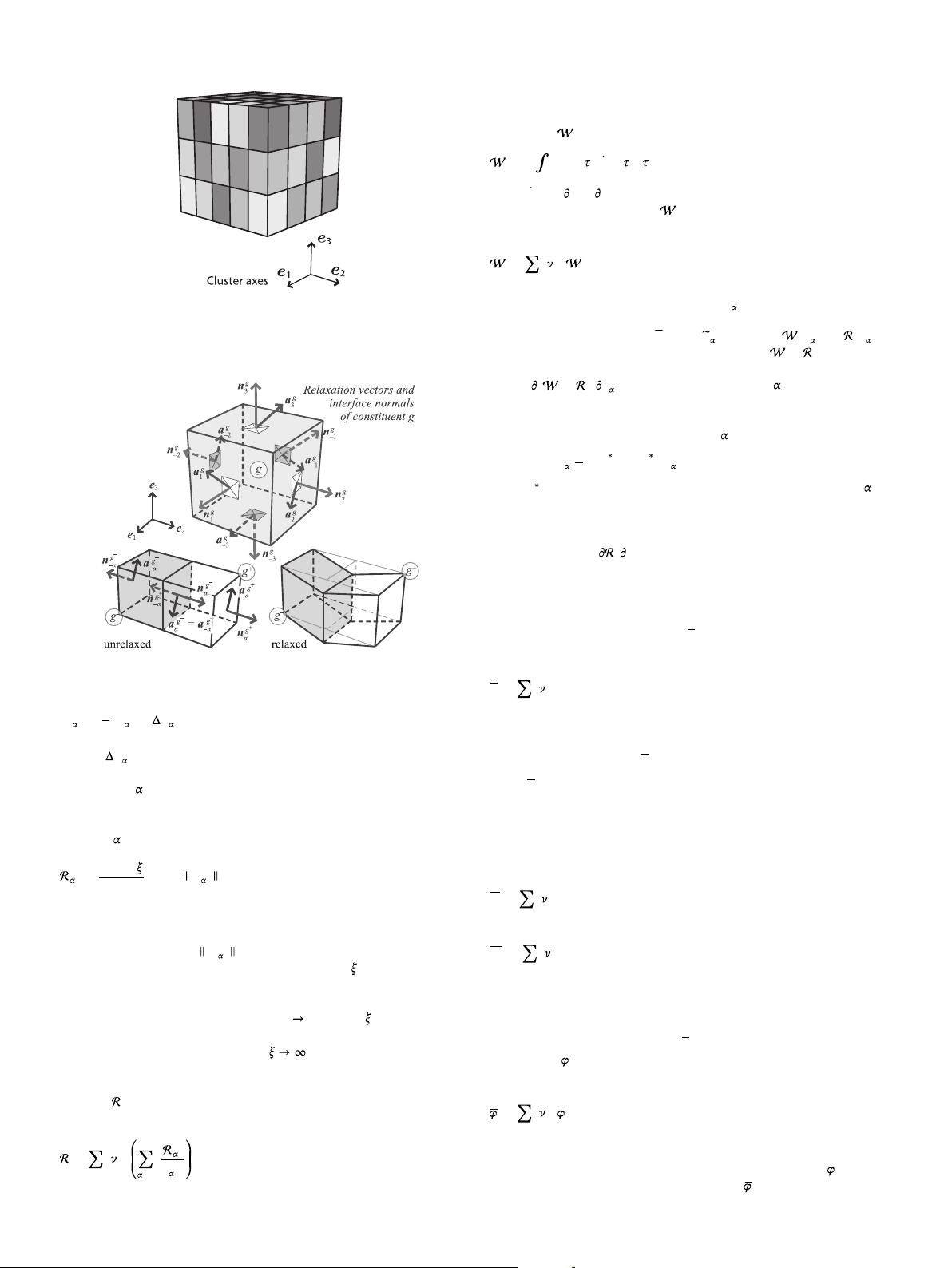
(43)

In general, diﬀerent ﬂuxes

g( )

and driving forces

g( )

will result in

the diﬀerent constituents. The ﬂux and driving force at the material

point are calculated as the average of all constituents:

f f

( )

(44a)

f f .

( )

(44b)

5. Single constituent kinematics

The intermediate C

ONSTITUENT LEVEL connects the PARTITIONING and

OMOGENIZATION and the CONSTITUTIVE LEVEL deﬁned according to the

hierarchical structure of DAMASK (Section 2.2). An abstract procedure

is established at this level to encapsulate all model-speciﬁc aspects in

the constitutive descriptions (Section 6).

The purpose of this level is therefore twofold: (i) to consistently

decompose the partitioned deformation gradient based on multiple

deformation sources and (ii) to integrate the internal state of the un-

derlying constitutive laws for ﬂuxes and sources over time. As outcome,

the stress and its tangent with respect to the deformation gradient are

provided to the P

ARTITIONING and HOMOGENIZATION level.

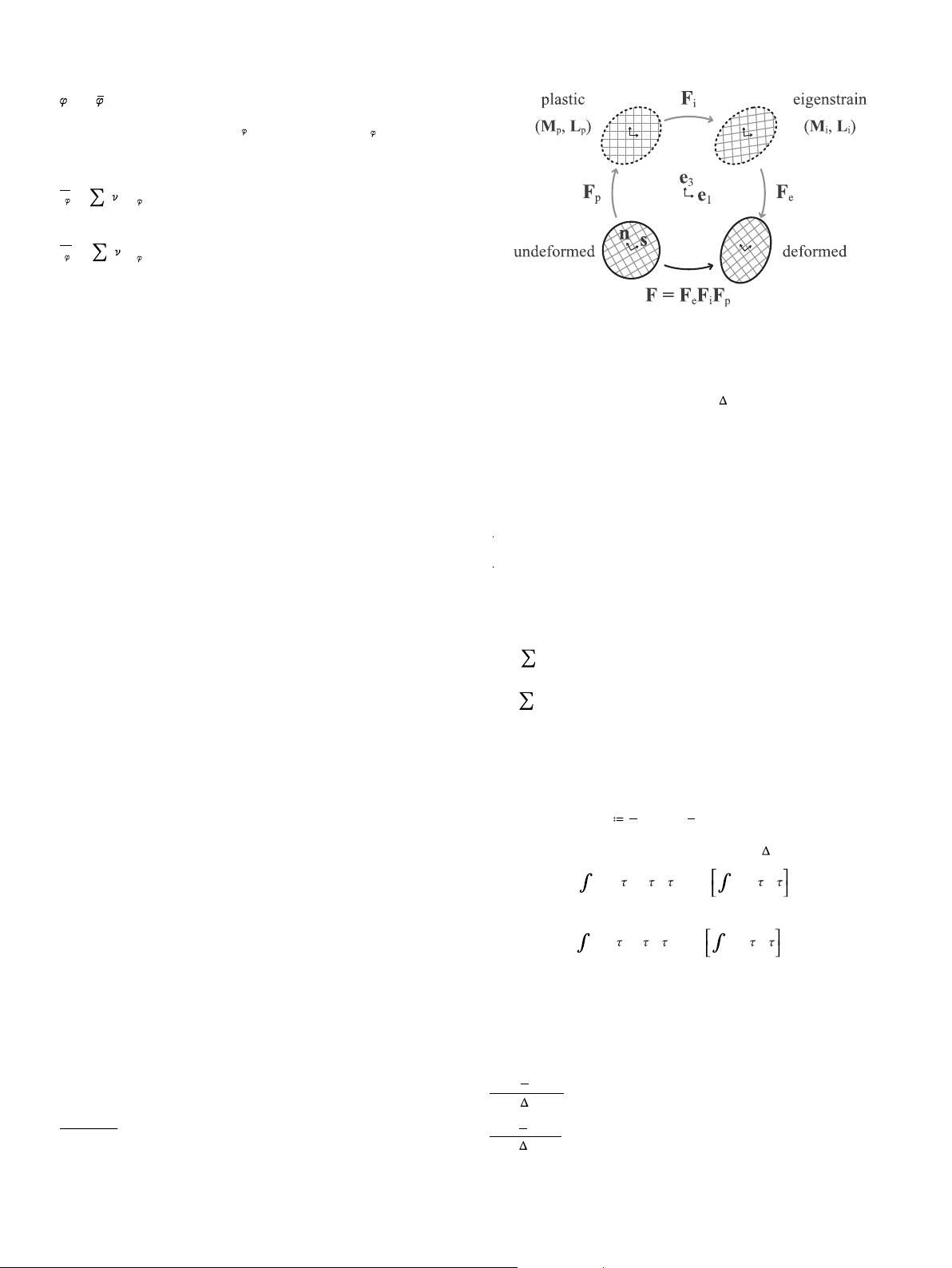
5.1. Multiplicative decomposition

The decomposition of the partitioned deformation gradient F is re-

quired to determine the stress response P.

The physical motivation for

this partitioning is a clear distinction between diﬀerent deformation

modes: Elastic deformation, resulting from stretching of atomic bonds,

plastic deformation, resulting from, for instance, dislocation motion,

and lastly eigenstrains, arising in connection with, for instance, da-

mage, phase transformations, or changes in temperature ﬁelds.

In the ﬁnite strain framework of DAMASK, the multiplicative de-

composition of the deformation gradient F reads as

=F F F F ,

e i p

(45)

where

is a lattice-preserving, inelastic deformation gradient that

maps to the plastic conﬁguration,

is a lattice-distorting, inelastic

deformation gradient, e.g. thermal expansion or crack opening [123],

mapping further to the eigenstrain conﬁguration, and

is an elastic

deformation gradient that maps from the inelastic to the deformed

conﬁguration. This decomposition is schematically shown in Fig. 4.

The speciﬁc order in Eq. (45) allows to conveniently account for

anisotropy, i.e. dependence on crystallographic orientation, of the

constitutive laws in the isoclinic plastic conﬁguration. To avoid un-

necessary rotations of tensorial quantities naturally deﬁned in the lat-

tice coordinate frame,

is initialized with the initial crystal orientation

, i.e.

= = = =t tF F O( 0) ( 0)

such that the plastic conﬁguration of

each crystal corresponds to a common cube orientation [65]. The cur-

rent crystallographic orientation O can then always be calculated from

through a polar decomposition

=F O U

, where U is the right stretch

tensor.

5.2. Time integration

The constitutive laws for inelastic deformation, i.e. the ﬂow rules,

are formulated in rate form.

This requires time integration of

kinematic quantities from

= +t t t

. In addition, for ﬂow rules

depending on an internal material state, this time integration has to be

performed consistently with the evolving state.

5.2.1. Inelastic ﬂow relations

The evolution of the inelastic deformation gradients

and

given in terms of their respective velocity gradients

and

by the

following ﬂow rules

=F L F ,

p p p

(46a)

=F L F .

i i i

(46b)

The inelastic velocity gradients are additively composed from in-

dividual contributions (indexed by n) and are driven by their work

conjugate stress measures, i.e. the M

ANDEL stresses

and

= …fL M( , ),

p p

(47a)

= …fL M( , ).

i i

(47b)

The M

ANDEL stresses

and

are calculated from the second

IOLA–KIRCHHOFF stress

(see Appendix C), which is determined by an

elastic constitutive law (Section 6.1) that expresses S as a function of its

work conjugate, the G

REEN–LAGRANGE strain E in the plastic conﬁguration:

= …fS E E F F F I F( , ), with

( ) .

e i

(48)

Integrating Eq. (46) over the given time interval

results in

= + =t t tF F L F L F( ) ( ) ( ) ( )d exp ( )d ( ) and

p p 0 p p p p 0

0 0

(49a)

= + =t t tF F L F L F( ) ( ) ( ) ( )d exp ( )d ( )

i i 0 i i i i 0

0 0

(49b)

and allows to solve Eq. (45) for given F.

5.2.1.1. Numerical solution strategy. The resulting closed set of Eqs.

(45), (46), (47), and (49) needs to be solved numerically. The exact

time integral of the velocity gradients (Eq. (49)) is approximated in an

implicit manner at a ﬁxed material state as

t t

F F

L F

( ) ( )

( ) ( ) and

p p 0

p p

(50a)

t t

F F

L F

( ) ( )

( ) ( ),

i i 0

i i

(50b)

which results in the inelastic deformation gradients at the end of the

time increment being

Fig. 4. Illustration of the intermediate conﬁgurations resulting from the multi-

plicative decomposition of the deformation gradient. Selecting the crystal orienta-

tion as initial value of

= =tF O( 0)

p 0

guarantees that the lattice coordinate system

in the plastic conﬁguration always coincides with the lab coordinate system [65].

The partitioned quantities

g( )

and

g( )

are, for brevity, referred to as F and P

in what follows.

In this setting, rate-independent models are expressed as the kinetic limit of

the corresponding rate-dependent model.

F. Roters et al.

Computational Materials Science 158 (2019) 420–478

430

=t t t tF I L F( ) ( ( )) ( ) and

p p

p 0

(51a)

=t t t tF I L F( ) ( ( )) ( ),

i i

i 0

(51b)

from which

can be calculated using Eq. (45). The linearization

procedure yields a system of nonlinear algebraic equations with three

unknowns

, and

. Its solution provides a stress state for a

consistent decomposition (Eq. (45)) that fulﬁlls the constitutive laws,

which are encapsulated as generic functions (Eqs. (47) and (48)) and

provided by the C

ONSTITUTIVE LEVEL (Section 6).

The solution scheme is implemented using a two-level pre-

dictor–corrector scheme for

and

(see Fig. 5), based on minimizing

the residuals

=R L L L L M L L( , ) ( ( , )) and

p p i p p p p i

(52a)

=R L L L L M L L( , ) ( ( , )),

i p i i i i p i

(52b)

where

and

denote the predicted values of

and

. The coupled

system of Eqs. (52a) and (52b) is solved using a modiﬁed N

EW-

TON

–RAPHSON scheme with variable step length α within a staggered

iterative loop until a consistent solution is achieved. The solution al-

gorithm is outlined in Algorithm 2. The N

EWTON–RAPHSON scheme is re-

garded converged when the residual drops below a given tolerance

= L Lmax( , , ) and

p a r p 2 r p 2

(53a)

= L Lmax( , , )

i a r i 2 r i 2

(53b)

that depends on speciﬁed values of absolute and relative errors (

and

Algorithm 2. Self-consistent integration of kinematic quantities at a

ﬁxed internal material state.

5.2.2. Internal material state

Above the C

ONSTITUENT LEVEL, the internal material state

is treated

as an abstract container that encapsulates all model-speciﬁc aspects of

its evolution (Section 6). The state

evolves simultaneously with the

kinematic quantities at a rate

= g S( , ).

(54)

In some cases, it might be necessary in the constitutive description to

express a change in the state in terms of an instantaneous jump rather

than by a rate of change. For this case, an additional rate-independent

constitutive equation is deﬁned:

= g S( , ).

(55)

The time integration of the inelastic ﬂow relations (Fig. 5) is stag-

gered with respect to the integration of

(Fig. 6). Diﬀerent schemes

can be used to accomplish the state integration. The following schemes

are implemented and a comparison of their performance within DA-

MASK has been compiled by Kords [124].

5.2.2.1. Fixed-point iteration. This implicit E

ULER scheme, used by, for

instance, Kalidindi et al. [125], iteratively evaluates the state and the

stress until a consistent solution is found. The residual (change between

iterations) of the ﬁxed point scheme is used as the convergence

criterion, however, a converged solution is not guaranteed. To

improve convergence and stability, the iterative state correction is

adaptively controlled in DAMASK. This time integration scheme will

always be ﬁrst-order accurate for the typical case of a viscous state

evolution. A schematic of the integration procedure is given in Fig. 7(a).

5.2.2.2. Explicit E

ULER integrator. This simple integration scheme

consists of a single explicit time step without any control of stability:

= + +t t t t t( ) ( ) ( ) ( ).

0 0 0

(56)

The stress is calculated after the state update, so that it is consistent with

the state. A schematic of the integration procedure is given in Fig. 7(b).

5.2.2.3. Adaptive E

ULER integrator. The explicit EULER integrator is

enhanced by using a second evaluation of the state integration to

estimate the error:

t t

( ( ) ( )).

(57)

This error estimate is used to reduce the time step in case a predeﬁned

tolerance is not achieved. Since a cutback of the time step would have

Fig. 5. Self-consistent integration of kinematic quantities at a ﬁxed internal

material state.

F. Roters et al.

Computational Materials Science 158 (2019) 420–478

431

剩余58页未读，继续阅读

chelle_njut

粉丝: 0
资源: 5

DAMASK：多物理场晶体塑性模拟工具

SpectralSolver _ Usage _ DAMASK.pdf

Python库 | damask-2.0.3.1406-py3-none-any.whl

PyPI 官网下载 | damask-2.0.3.1406-py3-none-any.whl

Python库 | damask_parse-0.1.5-py3-none-any.whl

DAMASK_GUI:杜塞尔多夫高级材料仿真套件的GUI

纺织面料英语词汇.doc

damask_parse-0.1.5-py3-none-any.whl Python库的安装与使用

精细金属掩模板(FMM)行业研究报告 显示技术核心部件FMM材料产业分析与市场应用

【创新未发表】斑马算法ZOA-Kmean-Transformer-LSTM负荷预测Matlab源码 9515期.zip

j link 修复问题套件

最新资源

精细金属掩模板(FMM)行业研究报告显示技术核心部件FMM材料产业分析与市场应用