《数字逻辑》教材前三章习题答案解析

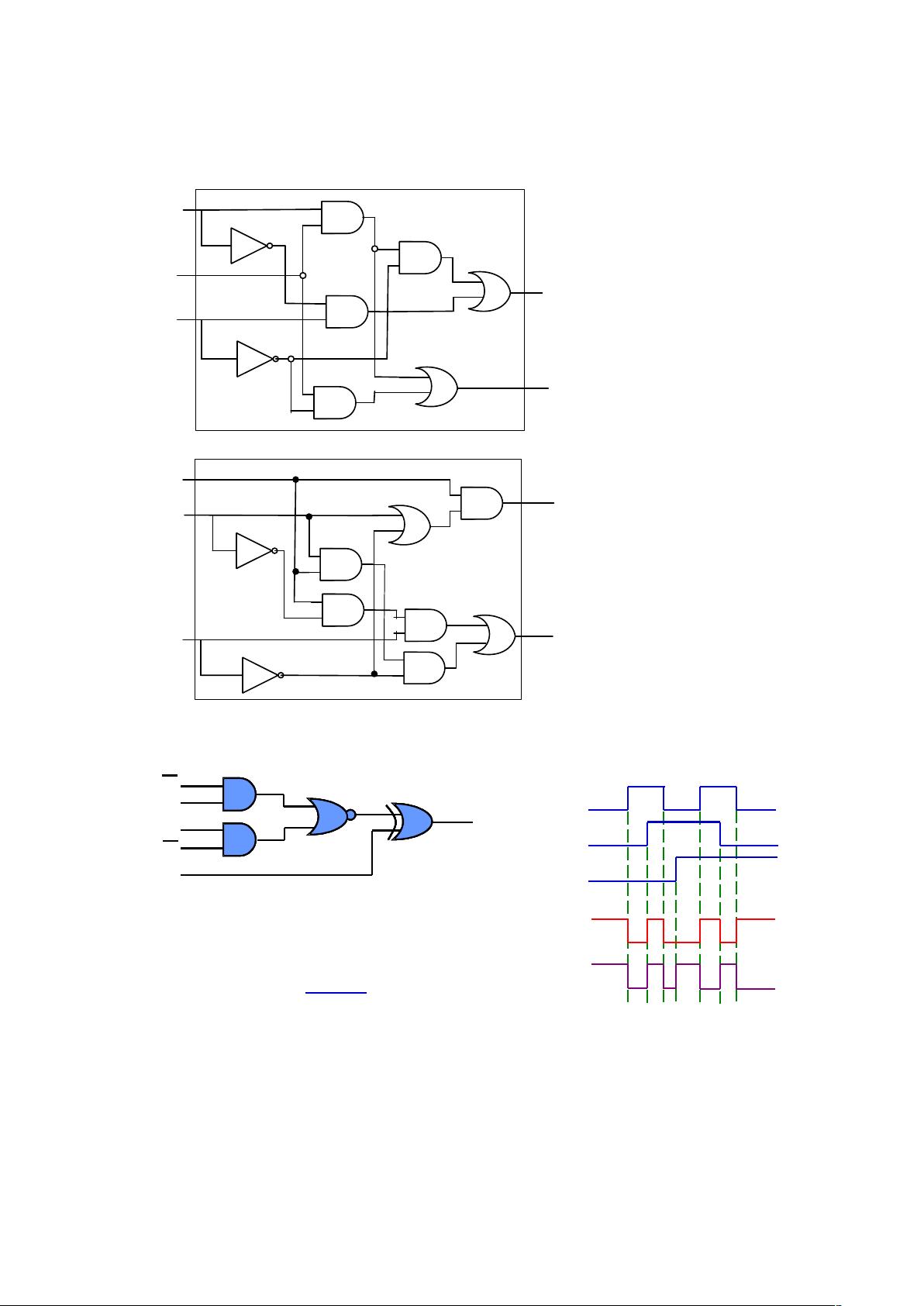
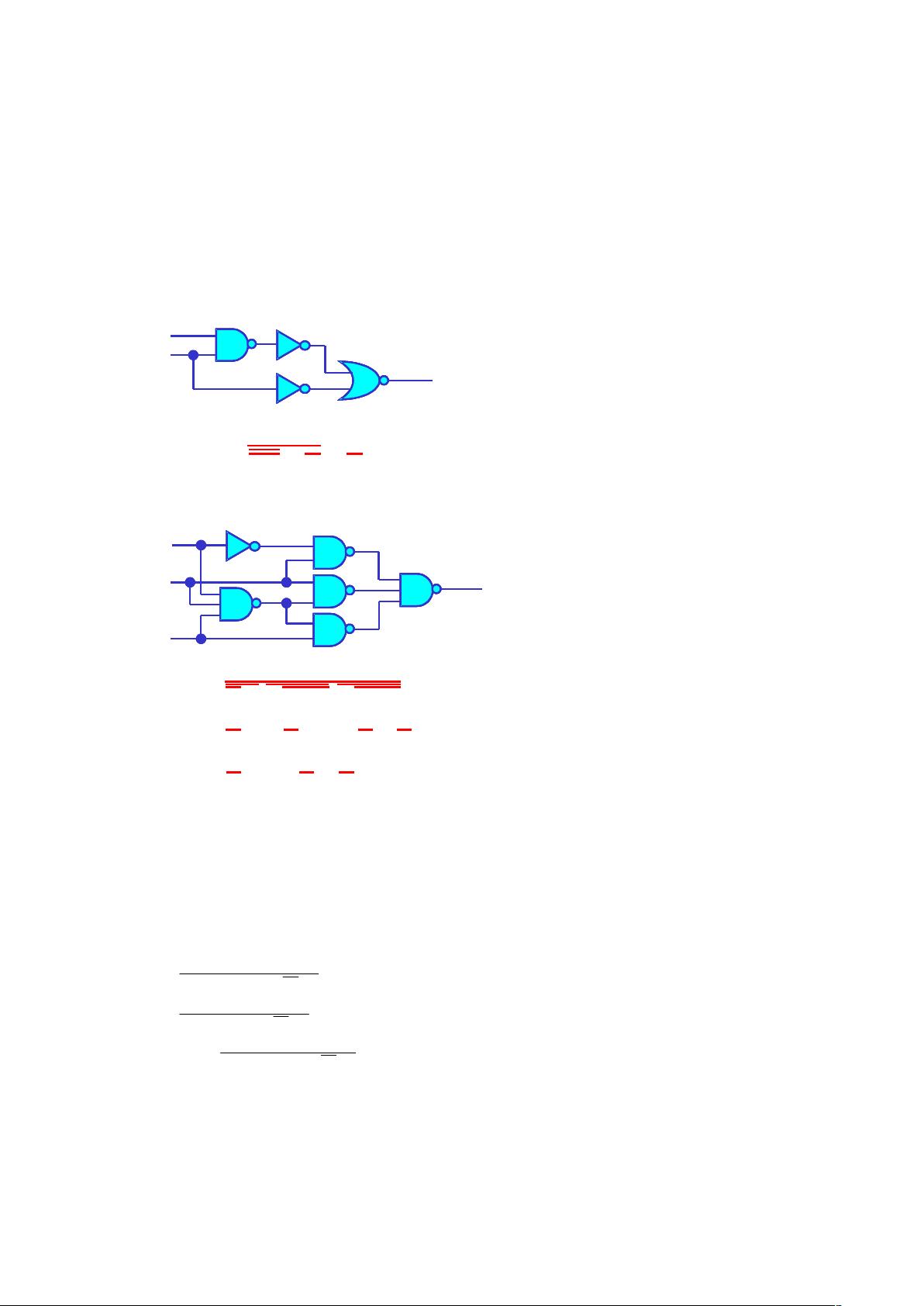
"《数字逻辑（第六版）》白中英等编著的教材前三章提供了丰富的数字逻辑基础知识，包括开关理论基础、组合逻辑和时序逻辑。文档为docx格式，大小为1.44MB，包含了相关章节的习题解答。" 在《数字逻辑》的前三章中，我们可以深入学习以下几个关键知识点： 1. 开关理论基础： - 数制转换：这部分主要介绍了如何将十进制数转换为二进制和八进制数，以及二进制数转换为十进制和八进制数。例如，49的二进制表示为110001，八进制表示为11001；1010101的二进制数转换为十进制是45，八进制是255。 - BCD码（8421二进制编码的十进制码）：用于表示十进制数的二进制编码，如1997的8421BCD码是0001100110010111。 2. 组合逻辑： - 真值表：通过列出输入变量的所有可能组合及其对应输出，可以分析和确定逻辑函数的性质。例如，题目给出了ABC和X的关系真值表，通过观察可得出X与ABC之间的逻辑关系。 - 真值表达式：根据真值表，可以推导出逻辑函数的表达式。例如，X=BC+AC+AB+ABC，这表示X的值依赖于A、B、C三个变量的组合。 - 逻辑函数简化：利用布尔代数定律，如分配律、结合律、德摩根定律等，简化逻辑函数表达式。例如，F=A+ABC+A+CB+=A+BC+。 3. 时序逻辑： - 时序电路：这种电路的输出不仅取决于当前输入，还与之前的输入状态有关。虽然题目未提供具体细节，但通常会涉及触发器、计数器和寄存器等基本概念。 - 时序逻辑函数的分析与设计：涉及如何根据时钟信号和状态转换来描述和构建时序逻辑系统。 4. 等式证明： - 恒等式证明：使用真值表或布尔代数定律证明逻辑等式的正确性。例如，(AB)C = A(BC)，可以通过列出所有可能的输入组合，验证两边的结果是否一致。 - 简化和化简：利用布尔代数定律证明两个逻辑表达式相等。例如，A+B=A+B，通过布尔代数的运算步骤可以证明这两者是等价的。 这些内容是数字逻辑学习的基础，掌握这些知识点对于理解和设计数字电路至关重要。通过解题和证明，学生可以深化对数字逻辑的理解，并提升逻辑分析能力。