数字信号处理实验:离散频谱分析与FFT应用
需积分: 0 157 浏览量
更新于2024-06-19
1
收藏 2.57MB DOCX 举报
该实验是关于数字信号处理的,主要涉及离散信号与系统的频谱分析,包括离散傅里叶变换(DFT)、高效算法(如快速傅里叶变换FFT)、线性卷积与循环卷积的关系以及DFT与FFT的运算时间比较。
1. **离散傅里叶变换(DFT)及其特性分析**
- 实验涵盖了不同类型的序列,如复序列、实序列、实偶序列、实奇序列和虚奇序列的DFT。
- 复序列的DFT不具备对称性。
- 实序列的DFT有共轭对称性。
- 实偶序列的DFT呈现实偶对称性。
- 实奇序列的DFT呈现虚奇对称性。
- 虚奇序列的DFT则有实奇对称性。
2. **高效算法计算2个N点实序列的DFT**
- 利用共轭对称性,设计了高效的算法来计算两个长度为N的实序列的DFT,通过与直接使用两个N点DFT的方法比较,验证了算法的正确性。
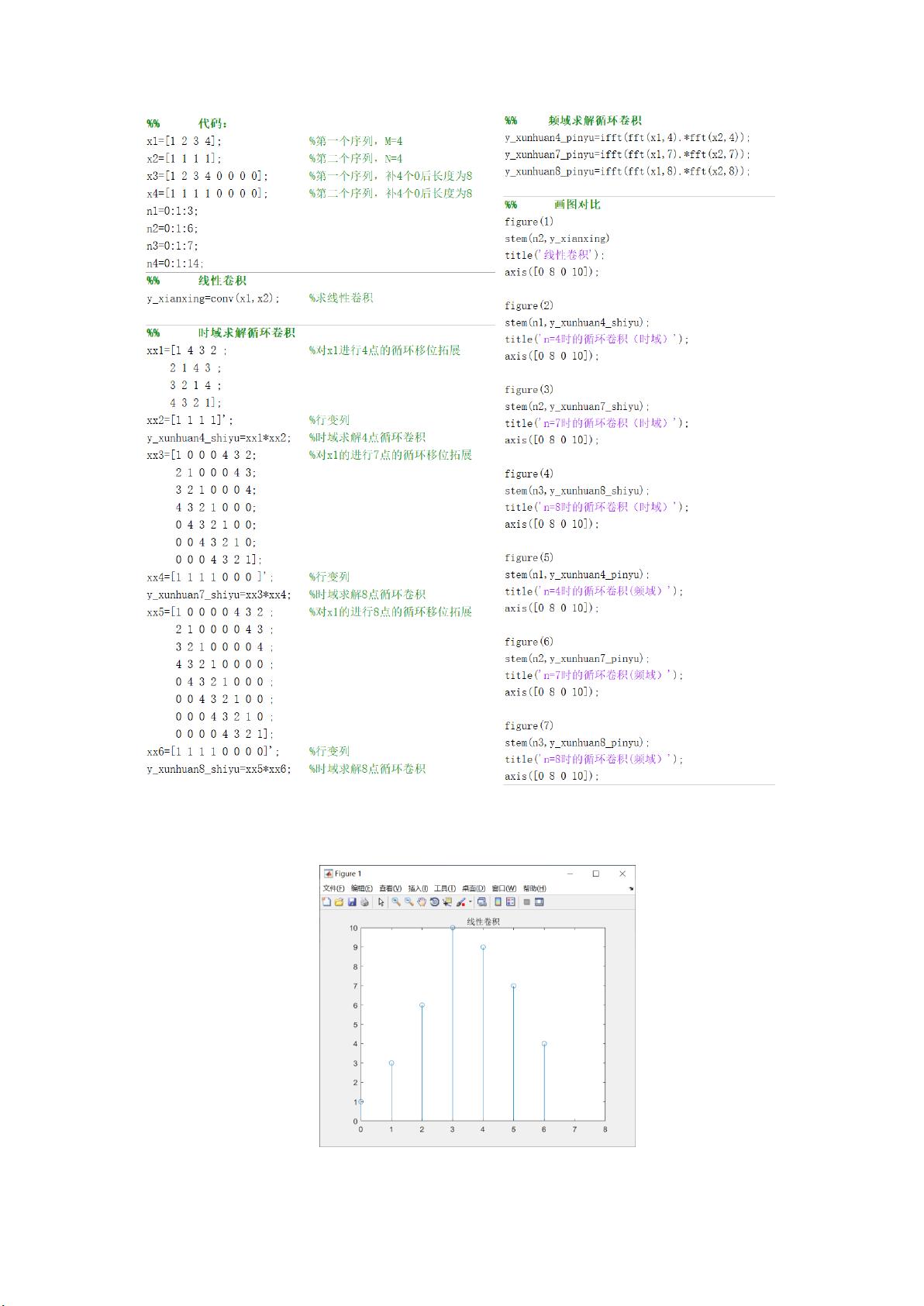
3. **线性卷积与循环卷积**
- 实现了两序列的线性卷积和循环卷积,循环卷积通过时域和频域两种方法计算。
- 分析了当循环卷积长度L与序列长度的关系,指出当L大于等于(M+N-1)时,循环卷积才等于线性卷积。
4. **DFT与FFT的运算时间比较**
- 选取不同点数N的序列,通过直接计算DFT和使用FFT函数,对比两者所需时间,证明FFT在运算速度上的优势。
- 随着N的增大,DFT的运算时间相对于FFT显著增加。
5. **频谱分析与采样频率、噪声的影响**
- 使用FFT求解信号频谱,讨论了采样频率如何影响频谱的解析度和准确性。
- 探讨了噪声如何干扰信号的频谱分析,强调了噪声控制在信号处理中的重要性。
这个实验提供了对数字信号处理核心概念的实践操作,有助于理解DFT的基本性质,优化算法的应用,以及卷积和频谱分析的关键概念。同时,它还强调了在实际应用中如何考虑运算效率和采样参数的选择。
5266 浏览量
2023-11-24 上传
2024-06-20 上传
160 浏览量
133 浏览量
252 浏览量

暗然而日章
- 粉丝: 600
最新资源
- MATLAB实现ART与SART算法在医学CT重建中的应用
- S2SH整合版:快速搭建Struts2+Spring+Hibernate开发环境
- 托奇卡项目团队成员介绍
- 提升外链发布效率的SEO推广神器——搜易达网络推广大师v2.035
- C#打造简易记事本应用详细教程
- 探索虚拟现实地图VR的奥秘
- iOS模拟器屏幕截图新工具
- 深入解析JavaScript在生活应用开发中的运用
- STM32F10x函数库3.5中文版详解与应用
- 猎豹浏览器v6.0.114.13396 r1:安全防护与网购敢赔
- 掌握JS for循环输出的最简洁代码技巧
- Java入门教程:TranslationFileGenerator快速指南
- OpenDDS3.9源码解析及最新文档指南
- JavaScript提示框插件:鼠标滑过显示文章摘要
- MaskRCNN气球数据集:优质图像识别资源
- Laravel日志查看器:实现Apache多站点日志统一管理