MOVING DS-OTHR ARRAY RECONSTRUCTION ALGORITHM BASED ON
INTERPOLATION
Ji, Zhenyuan, Ding, Jia, Xie, Junhao, Lu, Shan, Jiang, Xi
Department of Electronic Engineering, Harbin Institute of Technology
jizhenyuan@hit.edu.cn, giantpandading@163.com, xj@hit.edu.cn, eidolonking@gmail.com
ABSTRACT
Distributed shipborne over the horizon radar (DS-OTHR) is
a new radar detection system that becomes a new research
direction of shipborne OTHR. Array reconstruction and
signal reconstruction are the key techniques in the radar
system. Reasonable reconstruction for moving distributed
radar receiving subarrays can realize accurate measurement
of target. In this letter, we propose an interpolation approach
for time-varying radar system where uniform linear
subarrays (ULSA) are on different baselines, and apply the
approach to different conditions.
Index Terms—distributed shipborne OTHR; array
reconstruction; virtual interpolation
1. INTRODUCTION
Distributed shipborne over the horizon radar (DS-OTHR)
consists of one-transmit-multiple-receive or multiple-
transmit-multiple-receive ship formation [1]. It has the
advantage of anti-interference and high angular resolution.
Array reconstruction and signal reconstruction are the key
techniques in the radar system. Array reconstruction needs
real-time determination of each ship’s instantaneous spatial
location and to complete spatial alignment according to
coherent signal processing. Signal reconstruction requires
time alignment based on the location of each ship before
reconstruction and the location after virtual interpolation [2].
If the radar system satisfies reconstruction conditions, we
can use the virtual receiving array after reconstruction to do
signal processing in order to get higher angular resolution.
Up to now, many direction-of-arrival (DOA) methods
such as root-MUSIC, ESPRIT, forward-backward spatial
smoothing have developed. But they rely on uniform linear
array (ULA), don’t work in arbitrary geometry. In 1992,
Friedlander [3] presented an array interpolation approach
which transforms the response vector of an arbitrary array to
that of a ULA over an angular sector interpolation. Then
Pesavento [4] and Lau [5] developed this method. At present,
the array interpolation approach becomes a mainstream in
array reconstruction [6].
In this letter, we consider a radar system composed of
uniform linear subarrays (ULSA). These subarrays are on
different baselines, and have a mutual movement. During
the observation each subarray may change its position in an
arbitrary but known way. We complete array reconstruction
with segmentation-based interpolation method which can
reduce SNR attenuation compared with traditional
interpolation method. As ships sailing, the relative position
between receiving subarrays changes, and the array response
vector changes. Time-varying conditions would affect
angular resolution in the stage of signal reconstruction. In
this letter, we set an integration time to remove the
influence.
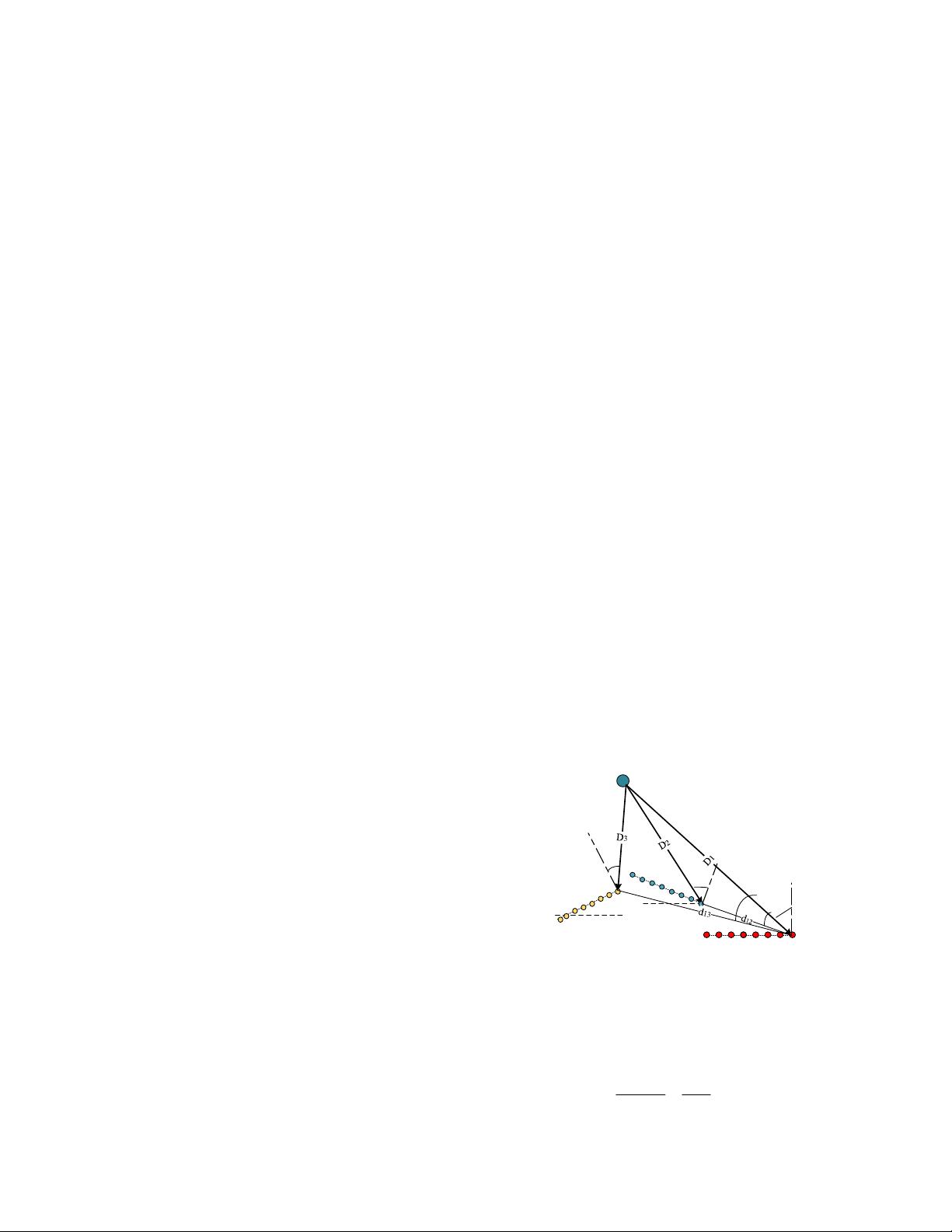
2. ARRAY SIGNAL PROCESSING MODEL
Consider three receiving subarrays on different baselines,
and each subarray is ULSA. Moving subarray response
vector is time-varying. The relative position of target and
subarrays are given in Fig.1, where r
k
(k=1, 2, 3) denotes
subarray in the radar system. “T” denotes the target.
Incident angle to subarray is given by θ
k
(k=1, 2, 3), and D
k
(k=1, 2, 3) denotes the distance from target to subarray. In
reality, D
k
is much longer. Before settling this model, it
needs to satisfy three terms: the number of sources is less
than the size of subarray, noise is white Gaussian and
uncorrelated in different moment.
T
θ
1
θ
2
θ
3
ψ
Φ
r
3
r
2
r
1
Fig. 1. The relative position of target and subarrays
Assume there are M
k
(k=1, 2, 3) elements in r
k
(k=1, 2,
3). Because subarrays are not collinear, r
2
and r
3
have delay
time compared to r
1
.The first element of r
1
is the reference
element as shown in Fig.1. The delay time is given by:
1
(2,3)
nn
n
DD D
tn
cc
−Δ
Δ= = =
(1)
978-1-4799-2186-7/14/$31.00 ©2014 IEEE









