蒙特卡罗方法详解：MATLAB应用与历史

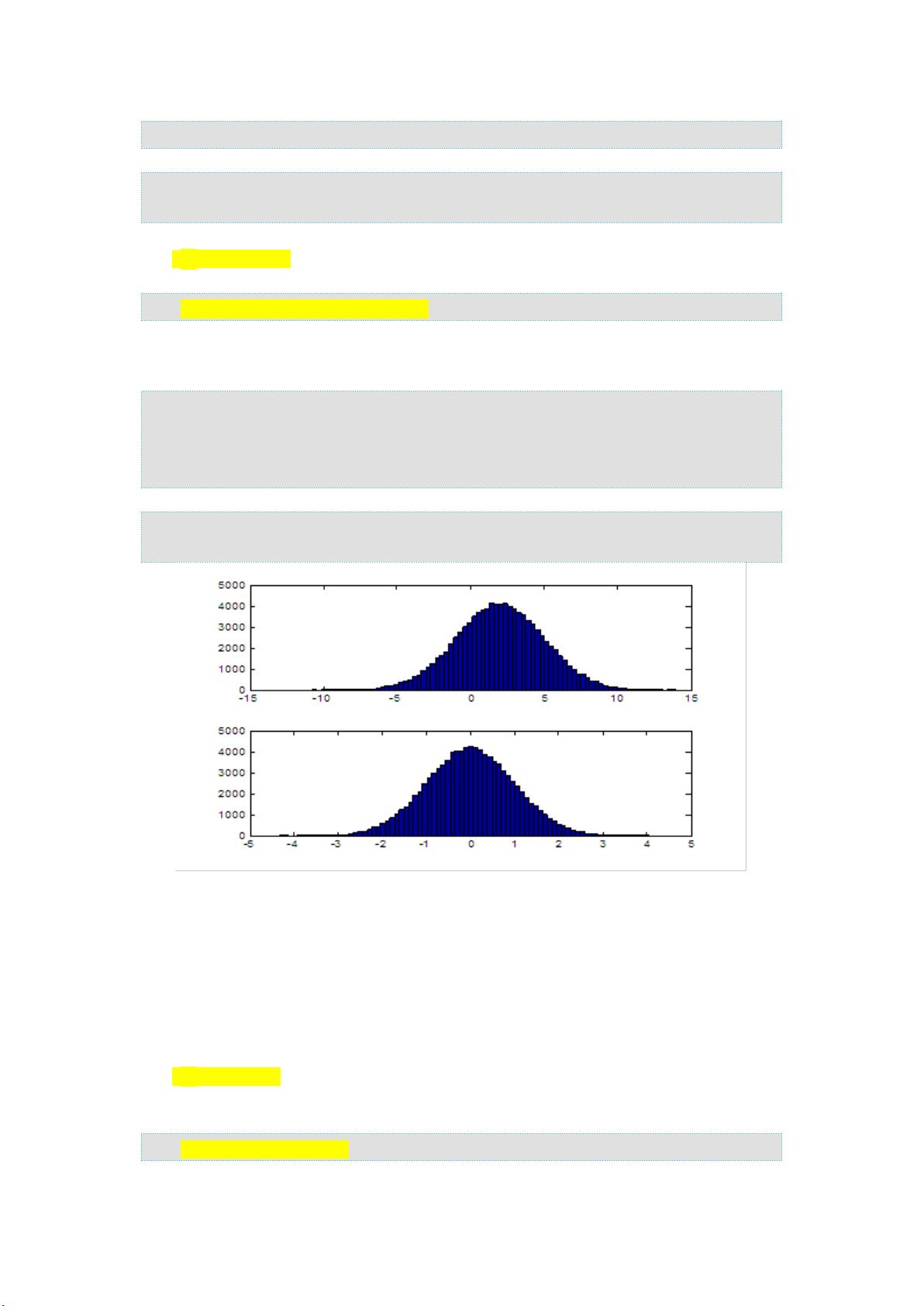
蒙特卡罗方法是一种基于概率论的数值计算技术，它的起源可追溯到18世纪末的投针实验，由布丰用来估计圆周率。该方法在二十世纪四十年代的美国原子弹计划中得到了广泛应用，因其保密性质，项目代号“Monte Carlo”由此得名，从此广泛传播开来。 蒙特卡罗方法的核心理念是通过大量随机试验来求解问题，尤其适用于那些难以找到解析解或求解过程复杂的数值积分问题。在传统的数值积分方法中，例如矩形法则或梯形法则，是通过将函数在区间上的分割区域面积近似相加。相比之下，蒙特卡罗方法并不直接计算每个小段的面积，而是通过随机采样在区间内生成大量的点，然后根据这些点落在某个区域的比例来估算积分的值。 例如，一个简单的数值积分问题可能是计算函数f(x)在某个区间[a, b]下的定积分为∫(a to b) f(x) dx。如果f(x)没有显式原函数，常规方法可能困难重重。然而，蒙特卡罗方法则可以通过生成大量的随机数x，计算f(x)在这些点上的值，并统计它们落在区间的次数，以此比例来逼近真实积分的值。随着采样点数量的增加，这种方法的精度会提高，误差逐渐减小。 此外，蒙特卡罗方法不仅限于数值积分，还广泛应用于各种领域，如金融风险分析、物理模拟、计算机图形学、机器学习中的参数估计等。它在现代信息技术中扮演着重要的角色，尤其是在处理不确定性问题时，由于其自然地处理随机性和概率性，成为解决复杂问题的有效工具。 在MATLAB环境中，提供了丰富的函数库和工具箱来支持蒙特卡罗模拟，用户可以根据需求编写脚本来实现各种复杂的计算和模拟任务。通过结合MATLAB的强大数据处理能力和可视化能力，蒙特卡罗方法的研究和应用变得更为便捷和高效。 蒙特卡罗方法在MATLAB中是一个强大的工具，无论是教学还是实际工程应用，它都提供了解决难题的创新手段，使得抽象的数学理论得以在实践中落地，推动了科学技术的进步。